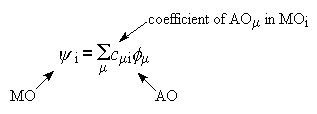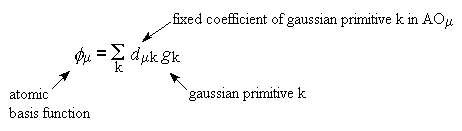Ab initio methods
-
You should read Chapter 6 of Goodman's 'Chemical Applications of Molecular
Modelling' from section 6.4.4 onwards, for an easy introduction to this.
(Before this is what you learned in stage 1.)
-
MO theory finds approximate solutions to Schroedinger's Equation, to get
energies and orbitals of electrons
-
Energies can be used for:
-
Geometry optimisation
-
Reaction energetics
-
Activation energies for kinetics (difficult)
-
UV/vis absorption prediction
-
Orbitals can be used for:
-
Graphical display (including assessment of where reactants might attack)
-
Charges
-
Dipole moments
-
Electrostatic potentials
-
NMR shieldings
-
Ab initio methods are available in many of the more expensive modelling
packages, or in Gaussian, which is available on a UCS unix machine
-
To do an ab initio calculation, you need to select:
-
The notation written in papers, and in the command line to Gaussian, is
in the form method/basis, e.g. RHF/3-21G* or B3LYP/6-31G*
Hartree Fock method
-
Abbreviation HF or RHF
-
Simplest method, closely related to what we teach in the stage 1 MO course
-
Good enough for most geometry calculations
-
May be good enough for reaction energetics
-
Just as geometry optimisations work by minimising energy with respect to
geometry, so ab initio calculations, for a single geometry
point, work by minimising the electronic energy by changing the array
of coefficients which control how AOs are added together to make each MO
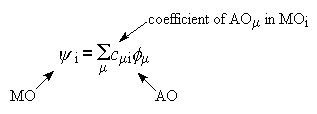
-
The Variation Principle says that if there are two approximations to a
wavefunction (i.e. two different sets of coefficients c), then the
better approximation is the one which gives the lower energy
-
The HF method works by calculating orbitals for one electron in an average
field of the rest, as follows:
-
Start with guess at the electron distribution
-
At the start of a calculation, this comes from a semiempirical calculation
-
Use the guess to calculate the average field of the rest of the electrons
-
Calculate coefficients to produce a set of one-electron MOs and energies
-
Fill the MOs according to the Aufbau principle and get total electronic
energy
-
Use this set of MOs as the next approximation to the electron distribution
-
Repeat the process with gradually improving MOs, until the electronic energy
converges, i.e. it changes by less than some pre-set limit
-
This is called self consistent field (SCF) convergence
-
If we are doing a geometry optimisation, the program moves on to the next
geometry point
-
The AOs move with the atoms
-
The set of coefficients from the last geometry point can be a starting
point for the new SCF calculation, and so on, until the geometry optimisation
converges
-
Because we have one iterative process, the SCF minimisation, inside another
iterative process, the geometry minimisation, the whole process takes a
lot longer than force-field or semi-empirical methods
-
The program can save a lot of time if it knows that all electrons are paired,
so it can treat them two at a time
-
This is so for ordinary, diamagnetic organic compounds, for most main-groups
compounds, and for organometallic compounds which obey the 18-electron
rule
-
This is called a restricted Hartree Fock treatment (RHF)
-
Treating compounds with unpaired electrons is much more difficult
Basis sets
-
The basis set is the set of AOs, which the HF method is going to find the
coefficients of, to make MOs
-
Schroedinger's equation can be solved exactly only for the H atom, so all
other AOs are approximations
-
The H-like orbitals we teach about in stage 1
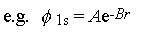 are called
natural orbitals
are called
natural orbitals
-
HF calculations involve calculating hundreds of thousands of integrals
in each SCF step, so it is important to use orbitals which are easy to
integrate
-
Natural orbitals are difficult to integrate, but Gaussian functions are
easier: the essential difference is that the r is squared
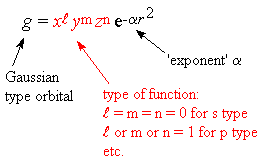
-
Gaussian primitives are added together in linear combinations to produce
basis functions which are approximations to natural orbitals
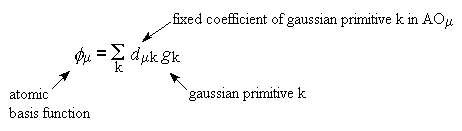
-
The designers of basis sets have optimised the set of coefficients d
and the set of exponents a used in the gaussian
primitives g to give a balanced set of orbitals for a certain set
of elements
-
There is a library of published basis sets on the web, but many of the
most useful are built into programs, so we need only give their name in
order to use them
-
The more primitive gaussians there are in a basis function, the better
the quality of the approximation, but the longer the calculations will
take
-
If the calculations take too long, e.g. more than a few days of processor
time on the computer we have access to, then this limits the size of molecule
we can tackle
-
There is always a trade-off between quality of basis set and practicability
-
You need to know 'what is the simplest basis set which will answer my questions'
-
Some programs allow professional computational chemists to design their
own basis set, but you must not, intentionally or accidentally, change
any of the numbers in a published basis set, otherwise your work will be
unpublishable because it could not be repeated
-
The way gaussian primitives are put together to make a basis function is
called a contraction, because a greater number of functions is contracted
into a lesser number
-
Contractions do not have to have a one to one correspondence with natural
orbitals, and they usually do not
-
If we have more basis functions than natural orbitals, then there are more
coefficients c to optimise in our SCF calculation, for our particular
molecule
-
This will give better quality MOs and energies, at the expense of a longer-still
calculation
-
The simplest basis set worth using in research is 3-21G
-
This means that core AOs are contractions of 3 primitive gaussians
-
Valence shell orbitals are each represented by two separate basis functions:
one is a contraction of 2 primitive gaussians, and the other is just a
single gaussian function
-
This is an example of a 'split valence basis set': the valence shell
orbitals are split into two components so that their shape can be varied
by taking different amounts of each component
You can see this by looking at the provided file '3-21G basis set for H,
C and N'. Open this in a separate browser window, so that you can
read these notes at the same time.
-
The first column of numbers with long decimal parts is the exponents a
-
The next column is the coefficients d
-
Hydrogen has just a valence shell, so we have two s-type basis functions,
one with two primitive gaussians, and the other with one
-
The three primitives have quite different exponents:
-
a big exponent gives a function which drops off quickly: this produces
the part of the orbital close to the nucleus
-
small exponents produce the part of the orbital further from the nucleus,
in the bonding region
-
Notice that the one-primitive basis function has the smallest exponent:
by adjusting the coefficient of this part in the SCF process, the program
can adjust the orbital in the bonding region
-
Carbon has a core 1s orbital, represented by three primitives
-
Notice the much bigger exponents than for H, because of the bigger effective
nuclear charge felt by core electrons, which makes them very compact
-
This particular kind of basis set saves computer time by representing both
s and p orbitals by gaussian primitives with the same exponents, but using
a different set of coefficients d for each usage. The first
column of coefficients is for making s orbitals, and the second column
for making p orbitals
-
The program knows it has to generate one s type orbital and three p type
orbitals for each of these sp entries
-
Nitrogen looks similar to carbon, except that the exponents are bigger
because the effective nuclear charge is higher
Polarisation basis function
-
Besides having two (or more) valence shell basis functions for each natural
valence shell orbital, to allow the tails of the AOs to be varied to account
for the different electronic properties of an element in different molecular
environments, you usually need at least one extra basis function to allow
the atom's electron cloud to be polarised off-centre from the nucleus
-
This is called a polarisation function
-
It is represented by a star after the name of the basis set, e.g. 3-21G*
-
A polarisation function is one orbital type higher than the highest natural
valence orbital, e.g. in general a p type gaussian is added to a H basis
set, a d type gaussian to a C basis set, etc.
-
The more sophisticated basis sets do that
-
Polarisation functions make little difference to simple basis sets for
small atoms like H or C, in which valence shell electrons are not very
polarisable, so 3-21G* has polarisation functions only for second row elements
such as P or S (or heavier), when d type gaussians are added
-
You must use a basis set with polarisation functions to model P-O, P-N
or S-O p bonding, otherwise you will predict
bonds which are too long and weak, and N will come out pyramidal instead
of planar, which it normally is when bonded to P or S
Higher ab initio methods
-
There are three kinds of error in using the Hartree Fock method with practicable-sized
basis sets
-
We would get a lower absolute energy, and better relative energies, if
we used a bigger basis set
-
As basis set size goes up, the energy converges to a theoretical limit
-
This unreachable limit is the 'Hartree Fock Limit'
-
When we look at single electrons in an average field of the rest, we take
no account of time dependence
-
The positions of individual electrons at particular instants are correlated
-
This error in the HF method is called 'Correlation Energy'
-
We have taken no account of relativity
-
Electrons move faster near to heavy nuclei, so their masses change
-
Important for heavier transition metals or heavy main group atoms, e.g.
Sn or I
-
There should be a relativistic correction
-
Altogether
ETrue = EHF practical
- Ebasis set error - Ecorrelation
- Erelativistic
-
A basis set error always has to be tolerated: the question is whether
to spend calculation time on a bigger basis set, or whether to spend it
on reducing the other errors by using a higher method. This kind
of question is discussed in Hehre's 'Practical Strategies for Electronic
Structure Calculations'
-
Some of the relativistic error can be removed by using Effective Core Potential
(ECP) basis sets for heavy atoms
-
Core basis functions are left out of the basis set and the effect of the
core electrons is represented by parameterised electrostatic potential
functions instead
-
The potentials can include a relativistic correction
-
Leaving out basis functions saves SCF calculation time, but calculating
forces for a geometry optimisation takes longer. These efficiencies
balance out for medium weight elements
-
ECP basis sets are quicker only for the bromine period and below
-
ECP cannot be used where core electron properties are required, e.g. for
NMR shieldings
-
What to do about correlation energy is the crunch problem
-
It is particularly important for loosely bound molecules, like transition
states
-
The traditional next method above HF is MP2
-
MP2 calculates a correlation correction after a HF calculation, but takes
much longer
-
Because it is slow, the MP2 method is only practicable for small molecules
-
MP2 is often used for single point calculations to get more accurate energies,
after geometries have been found at the HF level
-
Since 1996, Density Functional (DF) methods are being used instead of MP2
-
DF methods calculate correlation, working directly with electron density
instead of with MOs
-
A DF method replaces HF, rather than being an additional step, as is MP2
-
DF methods often contain a certain number of preoptimised parameters:
these are not changed by the ordinary user
-
The most popular DF method for organic molecules at present is B3LYP
-
Since 2000, we are finding that MPW1PW91 is better for inorganic molecules
-
These (and other) DF methods are built into Gaussian and some PC packages,
and are called up by name
-
DF methods are quicker than MP2, but may be less accurate
-
For moderate sized molecules, they are always slower than HF, but for large
molecules they should be faster, if used with the same sized basis set
-
DF does not always produce better results than HF, though it usually takes
longer: properties such as NMR shieldings may be predicted more poorly,
especially for lighter elements
-
DF methods are usually better than HF for calculating small energy differences
-
Some journal referees think HF methods are old-fashioned, and require authors
to at least try DF methods