Energy minimisation used to optimise geometry

• How does the minimisation routine find its way to the most stable structure?

 
• You should read Chapter 3 of Goodman's 'Chemical Applications of Molecular Modelling' about this


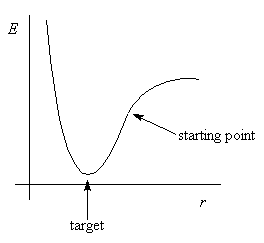
• Suppose we are minimising a diatomic molecule
• This is a one-dimensional minimisation:  energy depends only on one bond length r
• Calculate slope at the starting point, dE/dr
• If positive, need to decrease r.  If negative, increase r
• A polyatomic molecule has 3N-6 internal coordinates, where N is number of atoms
• Therefore have to minimise in 3N-6 -dimensional space
• First derivative of energy with respect to distance, dE/dr, is a force
• Instead of one force, we will have a whole array of them:

dE/dr₁, dE/dr₂ ...
• This defines a vector which tells us relatively how much and in which sense to alter each dimension in the next step, to go in the direction of steepest descent
• Actual size of step taken is reduced as forces get smaller, near bottom of valley

How does the program know when it has arrived?

• Should be negligible forces to go anywhere else
• The next step to be made would be negligibly small

What can go wrong?

• For a large molecule with several rotatable groups where there is little hindrance to rotation, the energy minimum can be very flat with respect to these rotations and accompanying breathing movements of the molecule
• The forces for going anywhere can be far smaller than the required maximum, but they still produce displacements which are too large
• Energies are probably good enough:  they are not changing much by then
• You cannot publish the results of a non-converged modelling experiment
• In some modelling programs, you need to be careful that you have not reached some built-in limit on the number of cycles, without actually reaching a minimum:  be careful to look at the text output
• You may be in a saddle point instead of a minimum
• Imagine walking down a hillside in thick fog
• You reach some level ground
• You do not know whether you are at the bottom of a hole, or whether you are in a pass, with a further drop-off to come
• If you are in a true minimum, all the force constants for vibration should be positive:  if you distort the molecule, it should fall back towards the minimum
• If you are in a saddle, then one vibration will go and not come back - it has a negative force constant, and the vibration is imaginary
• Good journals often require you to calculate vibration frequencies to make sure that none are imaginary, before they will publish a calculated geometry
• You may be in a small minimum of little chemical importance, even though it is a true minimum
• The structure may look very reasonable but there may be one or more much more stable ones you have not thought of
• For this you need at least a human protocol of  Conformation searching :  it is not permissible to do nothing but hope you have landed on the required model
• The bigger modelling packages may provide automated conformation searching, so that this can be done objectively