1. What We Choose & the implications: - the principle of trade, specialisation & comparative advantage.
2. Microeconomics of Trade - how different markets for the same goods interact.

Se, we are economical.  We concentrate on a very simple economy: one with only two factors of production (land and labour), which is only interested in producing and consuming two goods (food (+fibre); clothes (+ shelter)).  These two goods, which can be thought of composites as indicated, comprise all the necessities of life, and are all this simple economy produces, or, for the present, wants to produce.  It is self contained and self-sufficient as a whole.
Our economy is a self-contained collection of producers and consumers - everyone is either one or both.

Notice - we are talking of an economy here - which might be a country, or a region, or a community or locality or village, or whatever. In the limit, such an economy could be as small as a self-sufficient, single and subsistence household.  It doesn't matter how big or small it is.  All that matters - for the moment - is that it is self-contained.  We will come to what can happen when two such economies meet and trade with each other below.  For the present, we just consider the logic of this single and simple economy as separate and self contained entity.

What options does our economy have?

• to produce food (and fibre), or clothes, or (more likely) a mixture of the two.
• to consume (use) food and fibre or clothes, or almost certainly a mixture of the two.

The diagram we will use relates production and consumption of one good (food (and fibre)) to the production and consumption of the other (clothes (and shelter)).  So we measure (illustrate) quantities of each good on the two axes:  quantity of clothes on the vertical axis and food on the horizontal axis - though it could just as easily be the other way round, it doesn't matter.  Get a bit of paper and draw this diagram for yourselves now.  Then read the following and trace the argument (logic) out on your diagram as you follow it through.

Now - you have a right angled diagram, with quantity of clothes on the vertical axis and quantity of food on the horizontal axis. Presuming that we can measure these quantities, and add up the total (production and use) of each by all the people we are looking at, we can mark a point in the 'space' defined by the axes as the quantity mix of clothes and food our economy is producing and consuming.  Do that.

What can we deduce from the choice of this bundle of goods which our economy/society has chosen?

To answer that question, we need to consider what options our economy has.

In the simplest terms, the options range between using all available production factors (land and labour) to produce food;  or to use all its factors to produce clothes. In fact, and sensibly, it chooses to produce our observed combination of the two goods. And, because our citizens are sensible, they will organise themselves to produce as much as possible of each good.  What?  How come we presume they are sensible?  Because (if you like) these are our ancestors, and they were sufficiently capable to both survive and persist long enough to reproduce - and we are the result. What about leisure and living?  Don't they take time and effort?  Yes, so our production possibility set will represent the quantities of the two goods our citizens are prepared to, are willing to produce, given that any production involves use of scarce (limited) time and effort, for which there are competing leisure (consumption) and recuperation (investment - see below) demands

So, following this logic, there is some upper limit to the amount (quantity) of each good our citizens are prepared to produce in this economy.  We can mark these two upper limits (F* and C*) on each of the axes of our diagram of the economy.  Producing F* means that will not produce any C at all, so quantity of C is zero when Food production is at F*, and vice versa. OK?

But neither of these extremes is likely to be a sensible choice for our people - they are much more likely to choose a combination of the two goods, as we observe them doing.  What are the production possibilities for mixtures of the two goods?  Suppose we start with the economy producing all food and no clothes (at point F*), and now ask ourselves how much clothing this economy could produce if it diverted some of its resources from food to clothes production.  How much food production would have to be given up to produce the first few units of clothes?  Probably not very much, since some factors of production (land and labour) is not very good for food production and would be much better at producing clothes.  Furthermore, some of our people would prefer to make clothes than produce food, so are likely to be better at producing clothes than food.

So, to begin with, moving from F* upwards and to the left to produce more clothes and less food, our economy could gain quite a lot of clothes without having to give up much food production.  Eventually, though, as we progressively cut back on food production in order to produce more clothes, we will find that we are having to give up more and more food for each extra unit of clothing production - as the extra resources we need to produce clothes are progressively better at producing food than clothes.  Eventually, we would wind up producing all clothes and no food - at point C*.

So, our production possibility relationship will be curved between F* and C*.  Make sure you follow this logic and the representation of it as the production possibility frontier (PPF) on the diagram .  This should be what you got on your own diagram as you followed the argument through.  If you didn't, why not?  Notice, it is frontier because this curve represents the maximum possible combinations of food and clothes that our citizens are willing to produce, given the land, skills, technologies and work preferences they have.

Notice, too, what this PPF means.  Suppose we start at point C* and then ask how many clothes we have to give up to produce some food.  Move along the PPF, and watch how much extra food we get as we give up limited quantities of clothes. (draw and imaginary triangle with the hypoteneuse parallel to and touching the PPF - i.e. with the same slope as the PPF - the vertical side of this triangle shows the amount of clothes we can exchange for the amount of food, which is represented by the horizontal side of the triangle - see?).
At first, close to C*, we only have to give up a little clothes for a lot of food - the slope of the PPF is quite flat.  In other words, the supply price (cost) of more food in terms of clothes given up (the opportunity cost, which here is the total cost of food production) is low.

But, as we progress down the PPF, the real cost of food  (its cost relative to everything else in the economy, which in our case is clothes) increases - the slope of the PPF gets steeper.  The cost of food production increases the more food we try and produce - the real supply curve for food slopes upwards.

Repeat this argument (logic) for the price of clothes in terms of food - you will get the same answer - the real supply curve of clothes also slopes upwards: the more we want to produce, the higher the cost in terms of foregone food production - the higher the real (relative) cost of clothes.

PPF Conclusions:

• The PPF shows the full employment capacity of the economy: inside it means unemployment; outside it is impossible (unless, that is, we add to the capacity of the economy - see below)
• So, it also shows the maximum real income our economy can generate, in terms of food and clothes mixtures.  Our producers are here not producing these things just for fun, they are producing them because they and their neighbours want them - the products are their income, their return for the work they do.
• The slope of the PPF measures the real supply price (the real cost) of producing each of the goods, in terms of the other.
• The supply curves for both products slope upwards - greater quantities supplied "cost" more per unit, in terms of the amount of the other good which has to be given up.
  

• By "investing in human capital" - improving the skills and productivity of our people - the labour, (and the consumers), or simply having more people.
• By investing in land to make it more productive (draining it etc.), or simply by taking over more land.
  
• By improving the effectiveness of our production systems - getting more out for the same level of land and labour input - improving efficiency, which means one or both of better management (ideally less management, since management by itself produces nothing), and better technologies.
• By investing in capital (tools, plant and equipment) which labour can use with the land to produce the goods.
• By combining these things so that work (production) becomes more fun and more respectable, so that people are more willing to work than before (a point seldom, if ever recognised in the textbooks)

What about the consumption or demand side?  Now we have to think about how to represent consumer choices about how much of each (food and clothes) they would like to have and enjoy.  Go back to your paper diagram.  Start with some mix of the two which represents one particular (and observable) choice (F1 of food and C1 of clothes) - a point (x) which will be in the middle of our diagram somewhere - it doesn't really matter exactly where. But, if you are drawing this on the diagram with the PPF on it (which you should now have labelled), you had better put your x somewhere on this frontier, hadn't you?   Why?

Otherwise you will be trying to consume mixes of the two goods you cannot possibly produce (x lies outside the PPF).  Or you will be wasting resources - x lies inside the PPF, which means leaving people and land idle and unemployed when they could be working, and working at something they would like to do, and earning a living, and producing something we want, and thus earning respect.

So, put your x on the PPF - anywhere else is daft, (or, as economists say, inefficient), so we would not expect people to choose it, unless they are so stupid as not to be human.  This point x represents the mix of clothes and food that the people in our simple economy choose for themselves - it is the one we would observe them at, if we could find this simple economy to look at, and measure properly without disturbing the people at all.

Now ask yourself how the consumers in the economy might judge other combinations or mixes of the two goods that they might have chosen instead of x (F1 and C1)?  How might they compare other possible points on this diagram with x?

Within reason, more of each good would typically be considered preferable to less of each of the two goods, especially as we have included capital in each, - right?  So we can identify the north east quadrant (all points above and to the right of point x) as a preferred set or zone of possible consumption mixes or 'baskets' of goods.  Draw this zone on your diagram now. 

And the south west quadrant (all points or good combinations consisting of less of both F1 food and C1 clothes) will be considered inferior choices or combinations for our consumer population.  Otherwise they would have chosen one of the points in this zone, and they did not.  Shade in this inferior zone in now.

So, somewhere in the top left (north west) and bottom right (south east) quadrants will lie a boundary which separates the preferred set of consumption mixes from the inferior set, compared with our initial combination x.  There will be a separation between mixes which are preferred and mixes of goods which are considered inferior - a separation zone or boundary along which our citizens cannot make up their minds about which mix is better and which worse - they are, in effect, indifferent between any of the mixes defined by this boundary or indifference zone.

This boundary will (has to) slope downwards and to the right, passing through our reference point, x.  And, furthermore, it will have to lie everywhere outside (above and to the right of) the PPF, and only touch the PPF at the observed mix (x).  Why? Because, if this society preferred any other possible mix (defined by the PPF), other than x, they presumably would have worked out by now how to choose this other mix. But they haven't and didn't, so the indifference boundary must lie outside the PPF - see? In logic (and 'fact' in our mind experiment), any point, other than x, which is either on or inside the PPF is revealed as necessarily inferior to x by the very 'fact' of the observed choice of x rather than any other possible mix.  QED. So, draw such a boundary on your diagram.

You have just drawn what economists call an indifference curve (or boundary) (let's label it I2) which indicates all those combinations of food and clothes which the consumers cannot judge to either worse or better than the one they chose initially (x) - they are indifferent between any of the combinations which lie on this boundary or curve.  So, you can now extend the shading of both the preferred zone and the inferior zone up to this boundary. Got that?  If not, go back and re-read the logic and re-draw your own diagram.

You should have got (most of) this diagram.  But you didn't get three curves, you only got I2.  So what are the other curves?  Well, what we are drawing here is a map of consumer preferences.  The further north east we go this map, the more preferable the bundles of goods become - bundles to the north east of x have a higher value to the consumers than bundles to the south west.  The indifference curve we have drawn is a contour line on this preference "hill" - a line joining together all those points (bundles of the two goods) which are considered of equal value by the consumers, the citizens of our economy.  So there are as many other contour lines as we care to draw on this preference map.  I have just drawn in two others, of lower value than I2, so I have labeled them I1 and Io respectively.

Now go back to point x.  Ask yourself how much food our citizens would be willing to give up in exchange for a little more clothes - move upwards and to the left of point x along the indifference curve, I2.  Why is it a curve, sloping downwards and to the right ('convex to the origin" (where the axes cross), in technical language)?  Think about it.

If you already have mix x, ask yourself how much F you woulod be willing to give up (trade) in exchange for a bit more C? The more of F you have, and therefore the less of C, the more likely it is that you will be willing to offer more F for a little more C - down in the right/bottom corner, you will be willing to give up a lot of F (long horizontal 'bit' ) for a little more C (short vertical 'bit), so the slope of the indifference curve here is likely to be shallow (flatter).  As we get more C, and thus less F, so the amount of F we are willing to trade for more C will get greater - the slope of the indifference curve will get steeper. Got that?  If not, try the experiment again, and take your time.

Why along the curve?  Because, if we move upwards and to the right of this curve, we are assuming that our consumers consider themselves to have suddenly become richer.  How come?  Because they can get to a preferred mix of both goods anywhere above and to the right of I2 - (I2 marks the boundary between the preferred set of goods and the set considered inferior.)  They choose x - because they could not get any mix of goods above and to the right (outside) I2.  If they could have, they would have, and x would be in a different place than we supposed. [This sort of analysis is known, in the textbooks as revealed preference theory for this reason - the choices people actually make reveal their preferences for what they want, and about how much effort they are prepared to put in (or goods they are prepared to give up) to get it]

Indifference Curve Conclusions:

An indifference curve also shows a constant real income level for our economy, where income is now defined as command over consumption (and investment) mixes ("demand income"), rather than as the returns from production.  Note, again, that this is not a distinction that the textbooks identify.  Why not?  The answer takes us into some even deeper conceptual water than we are already in, and I don't think is necessary here.

So, if we want to know how much food our consumers will be prepared to give up (pay) for an additional quantity of clothes, we had better hold their demand incomes constant - otherwise we will confuse ourselves about why they are willing to pay more or less for more clothes - mixing up the effect of having more income with the consequences of a change in the terms of trade or exchange - otherwise known as the price - actually the real (relative) price - as the rate at which we can expect to exchange (barter) one unit of one good for a unit of another.  So we move up the indifference curve I2.  As we do so, what do we see?  That our consumers are willing to give up progressively less and less food for more and more clothes.  The indifference curve gets steeper.  The more clothes they want, the less food they are prepared to trade (pay) for them, the demand curve for clothes is downward sloping.

Alternatively, move down the indifference curve from point x.  The consumers are willing to give up less and less clothes for more and more food.  The indifference curve gets flatter.  The more food they want the lower the price in terms of clothes (the real price) they are prepared to pay.  The demand curve for food is downward sloping.

The slope of the Indifference Curve shows the real demand prices (the prices people, as consumers or users, are willing to pay) for the two goods. These are indeed real prices - each is priced relative to the other (which is all there is in this simple economy).

As the markets (the possible trade-offs) for each of the two goods settle down to their equilibrium positions, each will settle on a particular quantity and a particular price - at which the supply cost equals the demand price (where the supply curve and demand curve intersect).  Where will this equilibrium quantity mix (of food and clothes) be on our production possibility frontier (PPF) and consumer preference map (indifference curve map) diagram?  What combinations (quantities) of the two goods would you expect this single economy to choose?  Think, before you read on.

Answer: first, it has to be a mix that our citizens are willing to produce - so the combination has to lie somewhere on the PPF.  But where? Where the consumers think they are getting the best value from their consumption - i.e. as high up the preference map as possible  - on the highest possible indifference contour or curve.  Which is a single unique point (X) as a combination of C1 clothes and F1 food.  This economy, or community, cannot do better than this on its own. Indeed, that is exactly the way we constructed this mind experiment, or simple description of the choices our simple society/economy make, which we observed in this experiment.

We should expect a sensible, coherent and communicative, and cooperative community to come up with this, given time and no interference from anywhere else.  This is how we would expect people to learn to behave, if left to themselves.  What?  No, you wouldn't expect this?  They will fight and bicker?  They will steal and thieve?  They will behave like children, then?  They won't grow up and be sensible and wise?  Why not, if we leave them alone, wouldn't we expect them to grow up and learn from their mistakes and work out how to do things better?  Isn't this what humans do, if we leave them alone?  If they don't, they will wipe each other out.  These people, in case you hadn't noticed, are our ancestors - so they didn't wipe themselves out.

OK, so I have altered the shape of the PPF here - the reason will become obvious in a minute.  For the present, just notice that this different shape reflects the capacity of the community, and its willingness to work at these particular activities - this one is better at producing clothes than food compared to the previous one.  Why?  because it has more labour and less land, perhaps, and clothing (and shelter) production is more labour intensive and less land intensive than food and fibre production. Or for a variety of other possible reasons, which you should think about.

At this unique point, X,  this single optimum (best possible choice) combination of food and clothes, the indifference curve and the PPF will be tangential to each other - they will have the same slopes.  In other words, at this point, the rate at which consumers are willing to give up one good in terms of the other (the slope of the indifference curve), which is the consumer demand price for each good, will equal the rate at which it is possible to supply one good in terms of the other - the supply cost of each good - the slope of the PPF.  At this point, and this point alone, the production value of the two goods will equal the consumption value.

What are these rates?  They are the real (relative) prices of each good in terms of the other.  The supply prices are equal to the demand prices at this general equilibrium in our two markets.  And the price ratio of one good in terms of the other is the slope of the tangent - the ratio of C0 to F0 in the diagram opposite -  the supply price ratio of the slope of the PPF equals the demand price ratio of the indifference curve.  So, this country's markets will settle down at a general equilibrium of producing and consuming at point X, = C1 of clothes and F1 of food.

"General Equilibrium" Conclusion:

The social organisation of production and consumption - the choices about what to produce and consume - how to have a life and earn a living, can be seen, described and analysed as Markets - the balance between supply and demand. In an ideal world, the relative prices (exchange 'rates' or terms of trade) between goods and services will indicate (and reflect) both the production possibilities, and the consumer (or user) preferences for the goods and services.

Markets can achieve the best of all possible worlds, in the real world in which we live. This is a fact of logic not just an assertion or an assumption.  It is true in principle.  And we, as humans, are uniquely capable of turning our principles into practice (or vice versa - deriving principles from the outcomes of our practiced practices) - that is what we do that makes us different from the animals.  If the real world does not live up to this principle in its practice, then we will work to understand why, and then work to fix it.  This is science and reason.  Anything else is idle speculation or fantasy.  Simple, isn't it?  Tough, isn't it?  Is this why people don't like economics?

Implications:
The market system rewards the owners of the factors of production - those who have the most land, the most capital and the labour skills best fitted, most well matched to the wants of society (the consumer) will earn the most production income, and thus get to exercise the most money votes about what is produced.   If you (land, labour, capital, or management) are useless, you won't get paid in this system, and you won't get the chance to exercise your consumption income. To him that hath shall be given - from those who are most able, but not (necessarily) to those who are considered most deserving.

So we would also expect our sensible human community to show some humanity and seek to soften the harsh realities of natural selection (since that is what this system really is).  Our community will also develop governance and redistribution (care) systems alongside its market systems.  Why? Because, some form of government is an essential complement to this trading system - the long arm of the law is necessarily attached to Adam Smith's invisible hand of the market - to outlaw theft, enforce contracts and protect property rights (whether these are common rights or private rights).  Once in place, such governments will also become responsible for managing the natural selection of the market - including acting as judge to redistribute losses and gains, and protect or support the less well off.  The humane economy will naturally develop gifts from those who have to those who have not, which will be outside the system of exchange portrayed here. But not independent of it, since the capacity to give depends on the resources one can accumulate and incomes one can generate.

We have not concentrated on either the sociology or the politics of our economy, our community, here - because this is an economics lesson.  But it is nonsense to pretend that these aspects of humanity do not exist, or that economics is fundamentally different and separated from them.  They have to fit, and the way they fit is through the governance (or management, if you prefer) of what is, essentially, a market system.

Finally - the benefits of "Trade"  - i.e. exchanges of goods between different economies/societies.
Now, at last, we are in a position to look at the benefits from trade.  Before we do, though, notice that all our analysis/experiment so far has actually already been about trade and exchange within a single economy - the benefits of specialisation and trade (doing what you do best, and exchanging the products for the things you need) are implict in getting the most/best out of what we've been lucky enough to have got - the economy of life and living. You don't have to like it, any more than you have to like gravity, but you can't live without it, and you can't, in this world and this life, get away from it. It's called survival (and prosperity) of the fittest. It may be a poor system, from where you sit or stand, but it's better than all the rest - and we may be sure that the rest have been tried by our ancestors, and they have either been found wanting, or they have developed to what we have now.

Suppose, now, we have another community (or country, if you prefer).  This second community -  2 - is different to community 1: it has more land and less labour.   The PPF for country 2 shows that the country is better at food production and not so good at clothing production as country 1.  But the preference maps are, for our purposes, identical for the two countries.  On its own, then, country 2 would choose to produce and consume C2 clothes and F2 food, at a real price ratio of C3/F3.

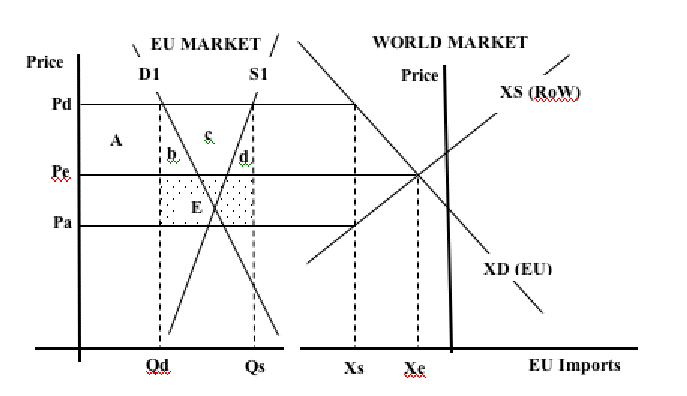
Now suppose you are a trader. You have an opportunity to do business between these two countries.  What are you going to do?  Buy clothes where they are cheap and sell them where they are expensive, and the same thing for food.  And where is food cheap?  In country 2 - you don't have to pay a much in clothes in country 2 as you do in country 1.  And clothes are cheap in country 1.  So there is money to be made shipping food from country 2 to 1 and clothes from 1 to 2 - right?  Just think about the meaning of the slopes of the "price lines" in each country - they show the price of one good in terms of the other.

And what happens when we start to trade - exporting food from 2 to 1 and clothes from 1 to 2?  The price of food will rise in country 2 (the food exporter), and the price of clothes will fall in 2.  Country 2's "price line" (C3 to F3) will get steeper.  The opposite will happen in country 1 - the line C0 - F0 will get flatter.

And what will limit this process of price changes as a consequence of trade between to two countries?  Again, from the previous session - the free trade or "world price" will be the same in each country - the slopes of the price lines will be the same, flatter than 1's and steeper than 2's.  The trading price line will lie between the price lines of the two countries, as in the figure below (Ce - Fe). I have omitted the previous no-trade price lines from these diagrams, to make them clearer.  But you should be able to re-draw these for yourselves.

So what? At this price ratio, country 1's optimum consumption point is now C1c of clothes and C1f of food.  This is where the trade price line touches the highest possible indifference curve. A higher indifference curve than it can possibly get to without trade - a higher consumer or demand income - so it is definitely better off with trade.

How does it manage to consume this amount of food (which is more than it could possibly produce itself in this diagram - C1f lies outside the PPF)?  Answer - it imports food, and pays for these imports with exports of clothes.

How much food and clothes would it pay country 1 to produce?  Where the trade price line is the same slope as (lies tangential to) the PPF - since the slope of the PPF shows the supply price ratio of the two goods - the price ratio which matches the opportunity costs of producing each of the goods.  So, country 1 produces P1c of clothes, and P1f of food, and trades (P1c - C1c) clothes for (C1f - P1f) food.

The exports [production minus consumption] of clothes pays for the imports (consumption minus production) of food, at the trading price ratio between the two products.  And country 1 is clearly better off with trade than without it, since it can now consume above (beyond) the limits of its production possibilities.  The same arguments apply to country 2.  Follow them through for country 2 for yourselves.

Conclusions from Trade:

• Country 1 is said to have a comparative advantage in clothing production - it can produce clothes relatively cheaply in terms of food, whereas country 2 has a comparative advantage in food production.  Notice, importantly, that one of these countries could be absolutely better at producing both goods - able to produce both more food and more clothes per person or per hectare.  But this would make absolutely no difference to its comparative advantage.  Unless both countries are absolutely identical (in which case their real prices would also be identical, and there would be no gain from trade, and thus no trade) , one must have a comparative advantage in one good and the other must have a comparative advantage in the other good - fact of logic; mathematical certainty; law of human nature - call it what you like.
• In particular - there is no way that one country can possibly have a comparative advantage in the production of both goods.  Having a comparative advantage in one good automatically means that the country has  comparative disadvantage in the other.  This result is perfectly general - it holds however many goods we might like to consider - any country will have a comparative advantage in something - something which it is relatively good at compared with all the other things it might be able to do. Comparative advantage relates your own abilities and capacity to produce one thing versus another, NOT you advantage relative to other people in producing either good.
  
• Trade allows these countries to exploit their comparative advantages, buying (importing) things which are relatively cheap from elsewhere and paying for these imports with exports of things which are relatively cheap in this country, and thus relatively expensive elsewhere.
• It will pay countries to specialise in the things which they are relatively good at - the things in which they have a comparative advantage.  Country 1 here specialises in clothes - producing more than it is willing to consume, and country 2 specialises in food (& fibre) production.
• Trade prices equalise between countries as trade occurs, which encourage the appropriate supply and demand responses to exploit these opportunities for specialisation
• The results of this logical analysis are unambiguous - trade pays and is of benefit to everyone.  There is no doubt about this - it is a fact of logic - it stands to reason.  Not believing this is exactly equivalent to not believing that the earth is round and goes round the sun - it is daft, nonsensical, illogical, without foundation.
• It is also, I argue, a fact of life as well as a fact of logic - because the principle of specialisation and trade according to comparative advantage is a basic principle of evolution and natural selection, and of life - how well off would you be if you tried to be completely, 100%, self-sufficient? How well off would your local community be? Your region be? Your country be?  Rabbits don't try to be wolves - they get better at being rabbits, and working better with the resources and conditions in which they find themselves. This is how natural ecosystems work, as well as how markets work.  But this is another story.

• Imports reduce the price of the good in the importing country (or region or locality) and increase the quantity which is purchased.
• Exports raise the price in the exporting region or location and reduce the quantity consumed (purchased)

Trade will be in equilibrium when it no longer pays to buy cheap and sell dear - in the limit, when the prices in the two markets are the SAME (apart from transport and marketing costs between the two locations - see below).  The process of trade can be represented through:

• Excess Demand (XD):  equivalent to the Demand for Imports - the difference between the quantity demanded and the quantity supplied in the local market at each and every price - which equals zero at the local equilibrium price (Pe in the diagram above), and increases as price is reduced below Pe - so  XD is Downward sloping.
• Excess Supply (XS): equivalent to the Supply of Exports - the difference between the quantity supplied and the quantity demanded in the local market at each and every price - which is zero at the local (autarchic - no trade) equilibrium price (Pu above), and increases as price is increased above this level - so XS is Upward sloping.

• In practice, there are costs of moving goods between different markets (especially over international borders), so prices of the same goods are not the same in different markets - they will generally be higher in importing markets and lower in exporting markets.
• The Importing price is often referred to in the statistics and trade press as the "cif" price - meaning that the cost of the good, insurance and freight charges are all included in the price.
• The Exporting price is often referred to as the "fob" price - meaning the price of the good free on board the exporting ship, having been paid for, but not yet moved.
• The difference between these two prices therefore reflects the costs of moving the good (more generally, moving and marketing it)
• Although this illustration is in terms of international markets, EXACTLY THE SAME PRINCIPLES APPLY to separated regional or local markets.