Calculation of electrical levels

Electrical levels

In the persuit of improved electronics, a significant problem is the engineering of materials that satisfiy the need for semiconducting materials with efficient doping. Most semiconducting material is deliberately chosen to be impure, mainly because one wishes to have material that has an excess of one type of charge carrier: electrons and holes.

The simplest dopants substitute for host atoms but have either one more or one less valence electron. A species with an excess of electrons is a donor (they donate these electrons to the aid conduction) and are "negative" in charge: this produces n-type material. Similarly, a deficit of electrons creates an acceptor (the species will accept electrons from the host) leaving a positviely charged valence-hole: this produces p-type material. Important devices (such as diodes) can be manufactured by the interfacing of n- and p-type semiconductors.

At zero-temperature, however, all these electrons and holes will remain on the dopants and the conductivity will be zero. As the temperature increases the fraction of donors or acceptors that are ionized (give up a carrier to the material) increases exponentially, the ionization fraction depends on the depth of the level from the semiconductor band-edge (see figure.1): the shallower the level, the more effective the dopant.

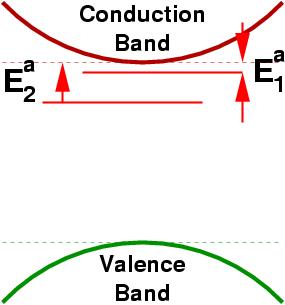
bandstructure
Figure 1: Schematic of an n-type semiconductor with two donor levels, Ea1<Ea2.

Formation energies

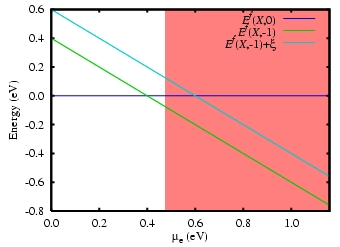
Formation energy plot
Figure 2: Illustration of the use of the formation energy to obtain an acceptor-level for the system X in silicon. Above the acceptor level X- is thermodynamically more stable that X0, whereas below the reverse is true. The shaded area indicates the region between the theoretical and experimental band-gaps. The inclusion of the correction term (greek character xi) in the charged formation energy pushes the acceptor-level above the theoretical value for Ec, but it remains deep in the experimental band-gap.

Donor and acceptor levels may lie anywhere in the band-gap. Technically, the question which we wish to answer is what are the range of the chemical potential of the electrons for which a given charge state is thermodynamically most stable? This question can be tackled by attempting to calculate the formation energy for each charge state:

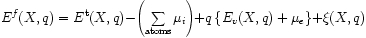
equation

The terms in this expression for system X in charge state q, in order, are the total energy taken from some calculation, a sum over the atomic chemical-potentials, an electroniv term (in braces) which accounts for the valence band top and chemical potential of electrons, and finally a term that accounts for a number of artifacts in the calculation of the first term arising due to, for instance, boundary conditions.

We calculate the formation energies for all possible charge states, and find which is the lowest energy for all values across the band-gap, as illustrated in figure 2.

Problems

However, using standard density-functional-theory (DFT) methods there are problems which make this calculation particularly challenging:

  1. Standard DFT methods drastically underestimate the band-gap. For example, germanium which has a band-gap of 0.7eV typically has a zero-band gap!
  2. When using periodic boundary conditions artifacts in the total energy due to dopant-dopant interactions can be very considerable. Even when atomic clusters are used, the defect-surface interaction and additional confining potentials can lead to large contributions.
  3. The location of the band-edges is ill-defined for systems including defects (eg dopants), especially in periodic boundary conditions. The average electrostaic potential can be corrected for, but it is not a clean result.
This means that the formation energy is difficult to establish accurately.

A potential solution: The Marker Method

One way around these problems is to assume that the errors are similar for comparable systems, and then take the bold step to simply cancel them: this is the marker-method. This method is very simple in that one takes two like systems, X and Y, for one of which the electrical levels are already known (Y), and this allows one to calculate the difference in the (say) acceptor levels:

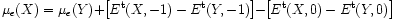
Marker Method Equation

Here the calculation only requires total energy difference involving the same charge state. Even if the band-gap is underestimated by 50%, it is in error by the same amount for X and Y, so the effect (largely) cancels.

However, for the errors to cancel to the best possible degree one requires:

  1. The electrical levels of the two systems are in the same region of the band-gap,
  2. the chemical and geometric natures are similar.
  3. and the perturbation to the bulk-like bands is minimized.
    4. However, even when these criteria are not completely satisfied, the degree of agreement one may obtained is very good.

Selected References

back