Doping for n-type diamond
Doping
Intrinsic semiconductors are characterized by an exponential dependence of conductivity with temperature, as electrons are excited across an gap in energy (the band-gap) where there are no states. Electrons in the conduction band, and holes (the absence of electrons) in the valence band can then move under an applied field giving rise to useful conductivity (see Figure 1).
Silicon is the most prevalent semiconductor technologically, but the band-gap of 1.16 eV would imply a very small number of conduction electrons and holes at room temperature.
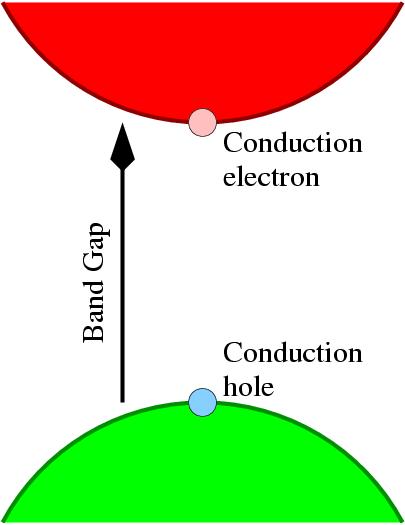
Figure 1: Schematic of an intrinsic
semiconductor.
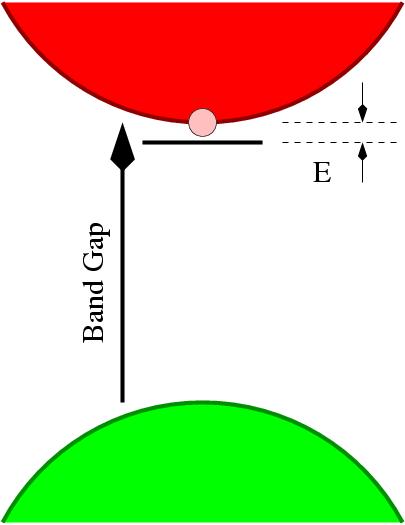
Figure 2: Schematic of an donor level in
n-type semiconductor.
Most semiconductor devices are manufactured from impure material, where the atoms in the host crystal are replaced by elements which have either more or fewer valence electrons. This is termed doping. At a simplistic level, one can view the impurity with one extra electron than the host (such as phosphorus in silicon) as being able to give up this electron to the conduction band (donate an electron) and then take no other role in the materials properties. Similarly, one fewer electron corresponds to a hole in the valence band, so the impurity accepts additional electrons. Donors give rise to so-called n-type material and acceptors p-type, with "n" and "p" standing for negative and positive, respectively.
Since the energy required to ionize a donor (E in Figure 2) may be very small, the number of conduction electrons can be made very large even at modest temperatures, and this process can turn an insulating material, such as diamond, into a conductive medium.
Doping in diamond
However, the presence of an impurity with an excess or deficit of electrons is by no means a guarantee of enhanced conductivity. For instance, nitrogen is one place to the right of carbon on the peroidic table, and hence has one more valence electron. One might then anticipate that substituting carbon with nitrogen would make diamond conductive, via the motion of free electrons in the conduction band. However, nitrogen substituting for carbon undergoes a distortion which generates a deep donor, i.e. the energy E in Figure 2 is large on a scale of kBT, a characteristic for available thermal energy.
The origin of the distortion may be viewed as a the preferential formation of lone-pair on the nitrogen and a dangling bond on one of its four carbon neighbours. This picture is confirmed by experiment which shows the unpaired electron is localized more on a single carbon atom than the nitrogen donor.
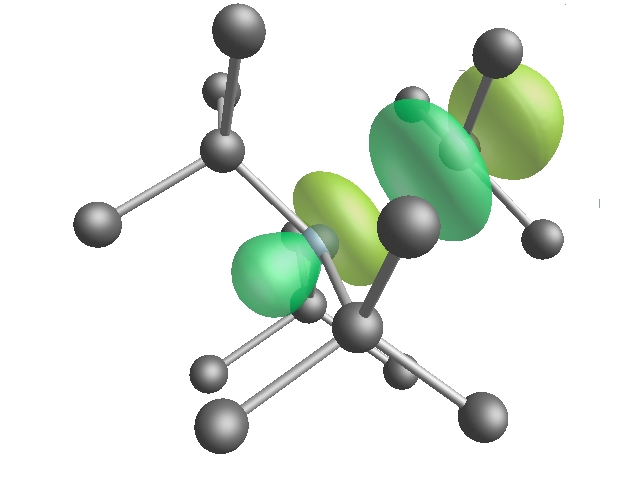
Figure 3: Schematic of the unpaired
electron on the deep nitrogen donor in diamond. The blue atom at
the centre is N. The different coloured wavefunction lobs are of
opposite sign but equal amplitude.
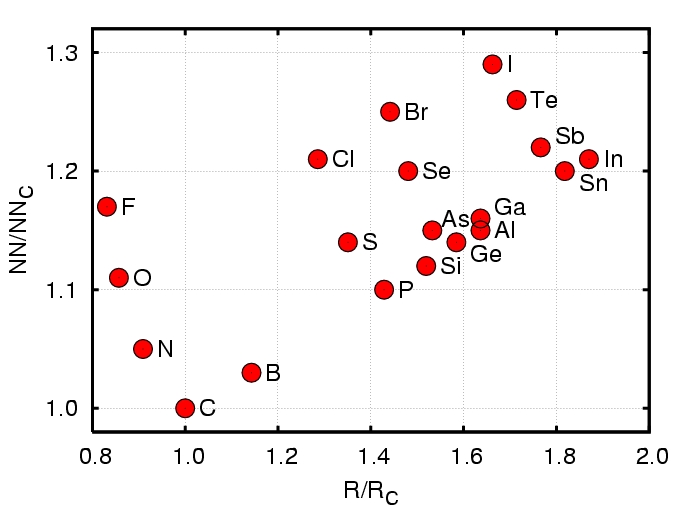
Figure 4: Calculated nearest-neighbour
(NN) bond-lengths versus covalent radii (R) for species in
diamond (taken from Ref [1]), each normalized
to the values for carbon.
Additional difficulty is found for n-type diamond from the small lattice constant: the range of impurities that will comfortably fit into the lattice is severly limited. We have looked at a wide range of impurity species and Figure 4 shows a range of published values. One important fact is that even for species with a smaller covlant radius than carbon, the surrounding lattice is pushe outwards. The greater the deformation of the bond-lengths (and angles) in the vicinity of the impurity, the greater the energy required to form the defect. This leads to the idea that the equilibrium solubility of dopants in bulk diamond is often very low.
However, phosphorus has been used successfully to produce n-type diamond, in the sense that the donor level (E in Figure 2) is much shallower than any other donor which can be reproducibly included in diamond. This qualification of the term success is very important: the donor level of P is relatively deep, at 0.6 eV below the conduction band. Therefore at room temperature the number of conduction electrons will be small as the fraction of donors that will be ionized depends on the exponential of the ratio E/kBT.
Is co-doping the future?
Two recent counter examples...
The race is on the find an alternative to phosphorus. This has led to a number of suggestions, many of which rely on the principles of co-doping. This essentially combines properties of more than one defect which conspire to yield the desired electrical (or indeed optical) properties. For example, the combination of two donors (D) and a single acceptor (A) in close proximity such as D-A-D will give rise to a single donor, but this may be shallower than that of an isolated single donor, D. Three suggestions along these lines are Si4N and B-H2.
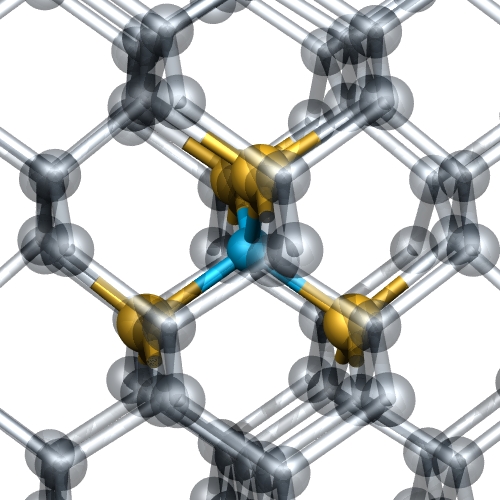
Figure 5:
Silicon-nitrogen complex proported to be a shallow donor in
diamond. The carbon atoms have been rendered transparent to
facilitate the view of the donor complex. The yellow and blue
atoms are Si and N, respectively.
1: Silicon-nitrogen complex
The idea [2] is that the confinement of the Si surrounding the N pushes the deep N donor level upward in energy. We find that for calculations involving larger numbers of atoms [3] that this is not the case. Indeed, the for C/N ratios exceeding around 200, the donor level of the Si4N complex lies close to or deeper than that of the intrinsically simpler phosphorus donor.
When computationally estimating the location of the donor levels, the role of system size and the details how the defect system is related to the bulk bands is very important.
2: Boron-hydrogen complexes
Boron is an acceptor in diamond (it has one fewer electrons than carbon). Indeed, boron gives rise to highly conductive diamond, and has recently been seen to be a low temperature super-conductor.
Boron-doped, p-type material in-diffused with deuterium has characterized by van der Paaws Hall measurements been interpreted to be n-type with a donor level half that of phosphorus (see [4]). The interpretation is that boron acceptors first trap a single deuterium atom, which passivates it (ie the boron-hydrogen complex acts as a carbon atom) and a second deuterium atom is then trapped to form a shallow donor.
Now, hydrogen is amphoteric (it can act both as an acceptor and donor), so treating interstitial deuterium as a donor gives us a D-A-D complex. The problem with this ivew is that theory predicts hydrogen (and deuterium) to be a very deep donor, so that the co-doping must give a very substantial shift of this donor level in order to explain the experiment.
Dai et al [5] reported calculations in support of such an effect. However, even they reported levels relatively far from the conduction band, and we found that their structures were unstable or high in energy [3,6]. Additionally, they appear to be insufficiently well bound to account for experiment. The most stable B-H2 defects we find behave like B-H+H.
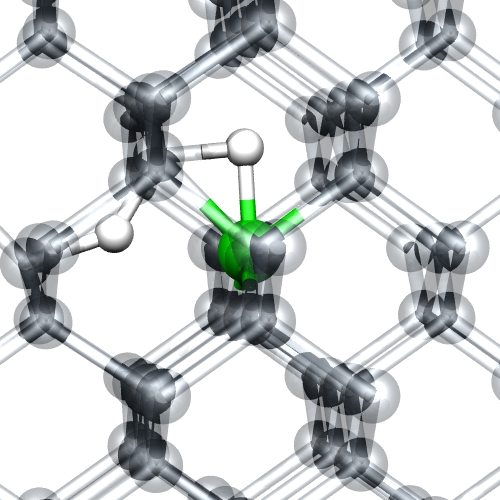
Figure 6: Boron-hydrogen
complexes in diamond. Green and white atoms are B and H,
respectively. The structure can be viewed as a passive B-H
complex adjacent to a hydrogen donor/acceptor (deep
levels).
Although co-doping has promised much, it has generally failed to deliver useful results. Infact there are several reasons why one might want to avoid this route if possible:
- The route to form complexes may require several processing steps.
- The individual ingredients may lead to unwanted compensation and hence additional charged scattering sites reducing mobility.
- Sometimes the useful form of the complex is one of several conformations, and indeed it may not be the lowest in energy. This means that the efficiency of shallow dopant formation may be low, or may reduce with operation.
- The thermal stability of the complexes may be inconsistent with operational lifetimes required for device applications.
- In materials such as diamond where very little diffuses without high temperature treatments, the only efficient way to co-dope is during growth.
- Implantation doping in diamond is problematic due to the difficulty in removing implantation damage which compensates donors [1].
Keep it simple!
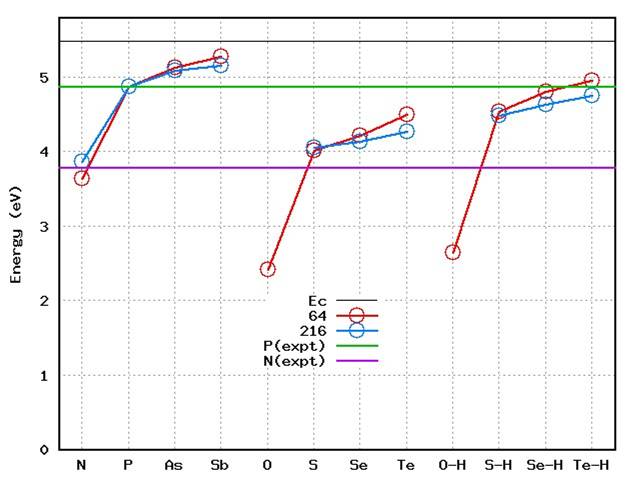
Figure 7: Calculated donor levels, relative
to phosphorus for pnictogens, chalcogens and chalcogen-hydrogen
complexes. Calculations performed in 64 atom 216 atom
supercells.
The complexity of co-doping and the relative simplicity of traditional doping mechanisms via single dopant species makes it highly desirabel to establish which, if any, chemical species will yield shallower donor levels than phosphorus.
We have found that although P is a deep donor, other pnictogens are better [7]. The distance between the conduction band minimum and the donor level (E in Figure 2) decreases from N to P to As to Sb. Now, it remains true that the size is also increasing so that the solubility of As is likely to be lower than that of P. However, it is clear that the concentrations of P obtained during growth is already far in excess of theoretical solubilities, so non-equilibrium surface effects are important.
Selected References
[1] JP Goss et al, Physical Review B 72, art. no. 035214 (2005)[2] D Segev et al, Physical Review Letts 91 126406 (2003)
[3] JP Goss et al, AIP conference proceedings 722 part A, pp.9194 (2005)
[4] Z Teukam et al, Nat. Mater. 2, 482 (2003) [5] Y Dai et al, Applied Physics Letters 84 1895 (2004) [6] JP Goss et al, Physical Review B 69, art. no. 165215 (2005)
[7] SJ Sque et al, Physical Review Letts 92 017402 (2004)