Dr R J Errington
CHY335 Molecular approaches to advanced materials. 11 lectures
What happens to material when light passes through it?
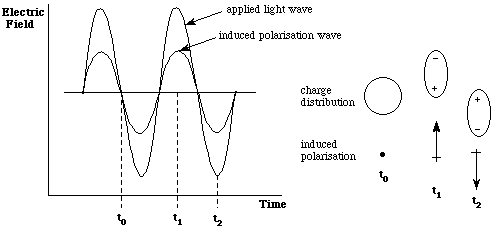
The electric field of a light wave interacts with the electronic charge of the material it is passing through.
At the atomic/molecular level:
This charge separation causes an induced dipole moment m proportional to the electric field E of the applied wave.
For small fields m(w) = a ij(w)E(w) where aij(w) is the linear polarisability at frequency w of the atom/molecule.
If the response is instantaneous, then the induced polarisation will be in phase with the incident radiation.

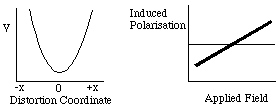
In this model, we are assuming the electrons to be bound by an harmonic potential where the restoring force on the electrons is linearly proportional to the displacement from the nucleus F = -kx
and the electrons see a potential energy surface defined by V = 1/2kx2
For the bulk material, the linear polarisation per unit volume at frequency w is given by
P(w) = cij(w)E(w)
where cij(w) is the linear susceptibility of the collection of molecules. The assumption is often made that the atoms/molecules are independently polarised by the light with no interatomic or intermolecular coupling, so that c ij(w) is related to the sum of all individual polarisabilities aij(w).
Displacement of the electronic charge in the material by the electric field E of the light creates a 'displaced' field D i.e. the total field within the material becomes
D = E + 4pP = E + 4pcE = (1 + 4pc)E
The dielectric constant, e(w) and the refractive index, n(w) of a material characterise its susceptibility.
The dielectric constant in a given direction is the ratio of the displaced internal field to the applied field (e = D/E) in that direction.
i.e. e(w) = 1+ 4pc(w)
What happens to the light as it passes through the material?
The light wave moves charge back and forth, as described above, and this motion of charge will re-emit radiation at the frequency of oscillation of the charge. For linear polarisation, this emitted radiation has the same frequency as the incident light. However, the polarisation changes the velocity of the light wave.
The ratio of the velocity of light in a vacuum, c, to that in a material, v, is the refractive index, n, of the material.i.e. n = c/v
At optical frequencies (far from molecular resonances), the dielectric constant is equal to the square of the refractive index. e(w) = n2(w)
We can therefore relate the refractive index to the bulk linear susceptibility
n2(w) = 1 + 4pc(w)
and since c(w) is related to individual atomic/molecular polarisabilities, this equation relates a property of light (velocity) to a property of electron density distribution (polarisability).
|
i.e. optical properties depend on electron density distribution that is dictated by chemical structure |
Non-linear Polarisability
So far we have assumed that the polarisation of a molecule or material is proportional to the applied electric field. However, when very high intensity electric fields are applied, a material can be sufficiently polarised that its polarisability can change.
If the electrons in the material experience an unsymmetrical potential energy surface (as in the figure below which has a cubic term included) the restoring force on the electron will no longer be proportional to displacement&emdash; it is non-linear.
At a first approximation (in 1 dimension): F = -kx - 1/2k´x2
The polarisation here depends on the direction of displacement.
[e.g. in the covalent C=O bond of acetone the electron cloud is more easily polarised towards oxygen].
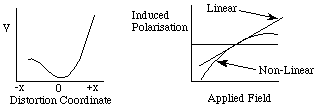
Just as linear polarisation leads to optical effects such as refraction, non-linear polarisation leads to non-linear effects but these are usually more subtle.
In the figure below, the application of a symmetric field (associated with a light wave) to the anharmonic potential field results in an asymmetric polarisation response. The maxima of the polarisation wave are greater in one direction than in the other.
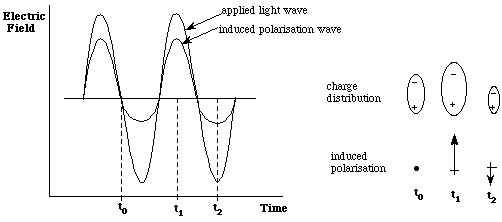
This asymmetric polarisation wave can be decomposed by Fourier analysis. As an approximation, the polarisability can be expanded as a Taylor series:
m = m 0 + (a)E + (b/2)E2 + (g/6)E3 + ......
The terms beyond aE are not linear in E and are therefore referred to as the non-linear polarisation and give rise to non-linear optical effects.
|
NB (i) Non-linear polarisation becomes more important with increasing E (therefore there were few observations of NLO effects before the invention of lasers with their associated large electric fields) (ii) Only molecules and materials lacking a centre of symmetry display 2nd order NLO effects. |
The observed bulk polarisation density is given by:
P = P0 + c(1)E + c(2)E2 + c(3)E3 + ....
where P0 is the intrinsic static dipole moment density of the sample.
What are the observable non-linear optical properties?
A classical oscillating dipole emits radiation at the oscillating frequency. For linear first-order polarisation the radiation has the same frequency as the incident light, but what is the frequency of the re-emitted light for a non-linear optical material?
Since the electric field of a light wave can be expressed as E = E0cos(wt), the expression for P can be written as
P = P0 + c(1)E 0cos(wt) +c(2)E02cos2(wt) + c(3)E 03cos3(wt) + ....
and since cos2(wt) = {1/2 + 1/2cos(2wt)}, the first three terms can be rewritten as:
P = {P0 + 1/2c(2)E02} + c(1)E 0cos(wt) + 1/2c(2)E02cos(2wt) + ....
This effectively means that the polarisation consists of:
(i) a second order DC contribution to the static polarisation [first term](ii) a frequency component w corresponding to the incident light frequency [second term]
(iii) a new frequency doubled component 2w
This is shown in the next figure.
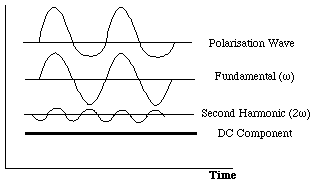
|
(second harmonic generation, SHG)
in addition to a static electric field (optical rectification). |