The Unintentionally Useful Consequences of Playing Games with Maths
Christian Perfect
About me
I did maths and further maths A-Level, then a pure maths Master's degree here at Newcastle.
I now work here in the School of Mathematics and Statistics, making a computer-based homework system, among other things.
but I also do recreational maths...
Yes, that's a thing.
The unplanned impact of maths
Surprisingly often, maths invented for no reason other than the fun of it turns out to be very useful.
Recently, I was playing about with a remarkably mathematical shape.
Platonic solids
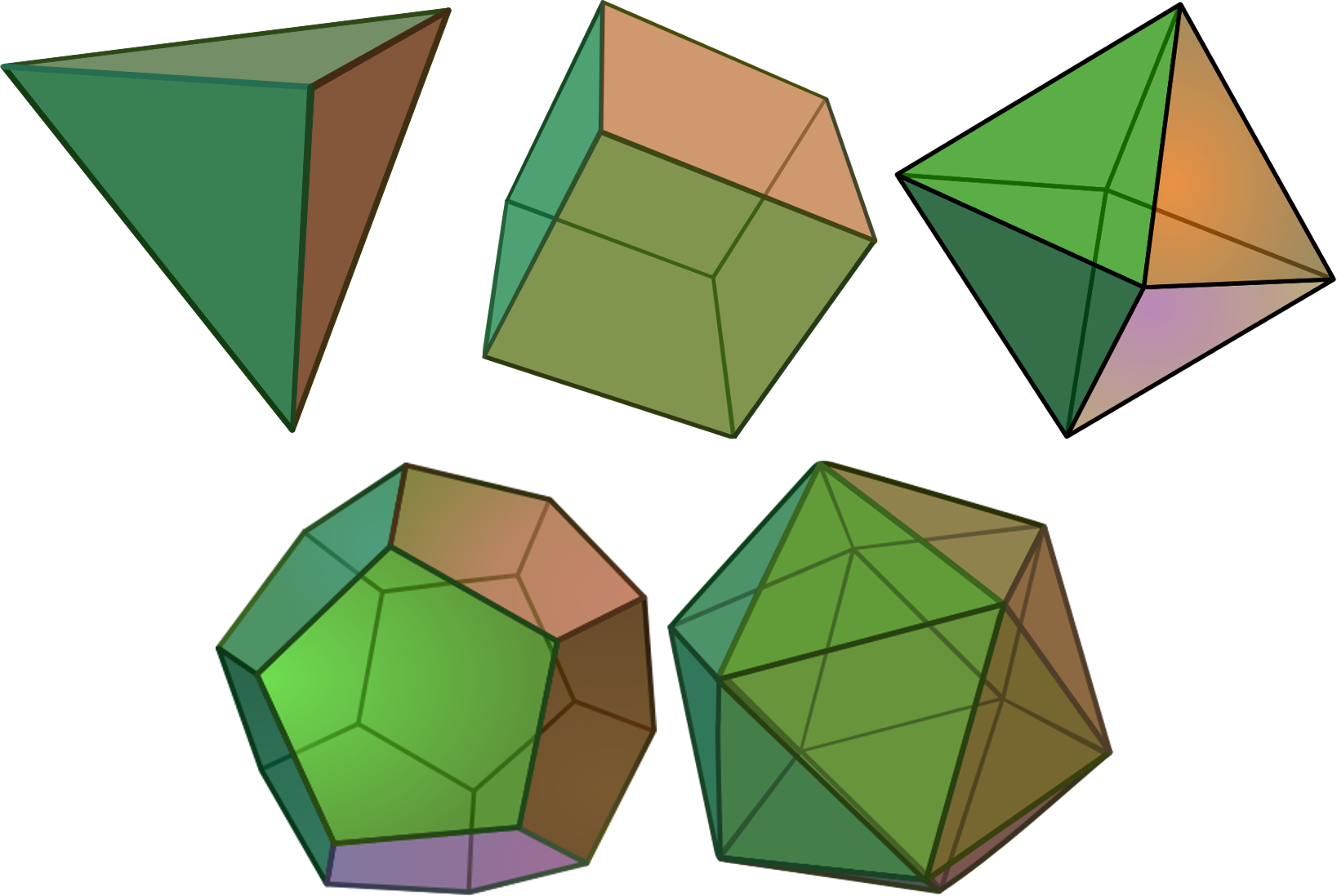
A polyhedron is a 3-dimensional shape with flat sides and straight edges.
A Platonic solid is a solid whose faces are all regular polygons, with the same number of faces meeting at each vertex.
What can we say about a polyhedron?
- Number of edges, faces, sides.
- Shapes of the faces.
- Symmetries.
Graphs
A graph is a collection of points (vertices), and the edges joining them.
It doesn't matter where the points are, or what shape the edges are.
What can we say about a graph?
- Number of vertices and edges.
- How many edges connecting each vertex?
What can we say about a graph?
Can you colour the vertices so that no two neighbours have the same colour?
or
Can you arrange the vertices on two sides of a line so that no edge stays on the same side of the line?
A graph with this property is called bipartite.
What can we say about a graph?
Can you draw a path which goes along every edge once, and ends where it started?
What can we say about a graph?
Can you draw a path which goes along every edge once, and ends where it started?
A graph with this property is called Eulerian.
The bridges of Königsberg
What can we say about a graph?
Can you draw a path which goes through each vertex exactly once, and ends where it started?
A graph with this property is called Hamiltonian.
A Theorem
Every bipartite graph with an odd number of vertices is non-Hamiltonian.
The Herschel graph
A colleague showed me the Herschel graph, and asked what I could do with it.
Unintentionally useful maths
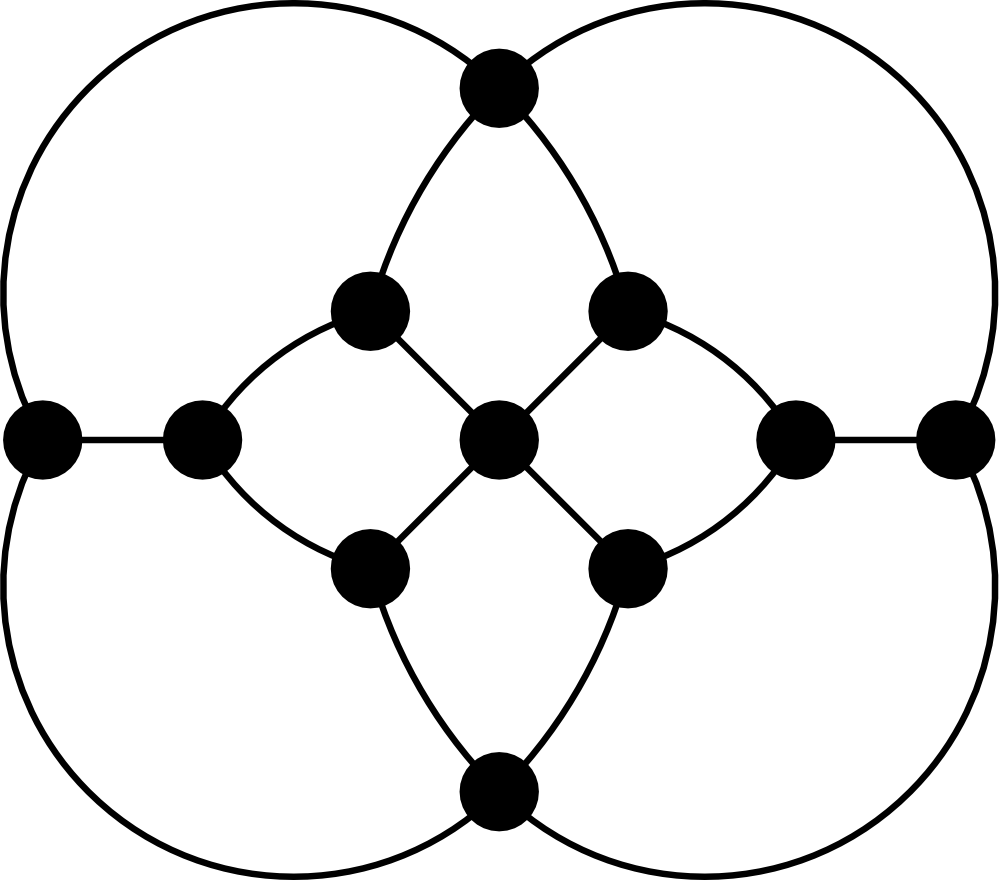
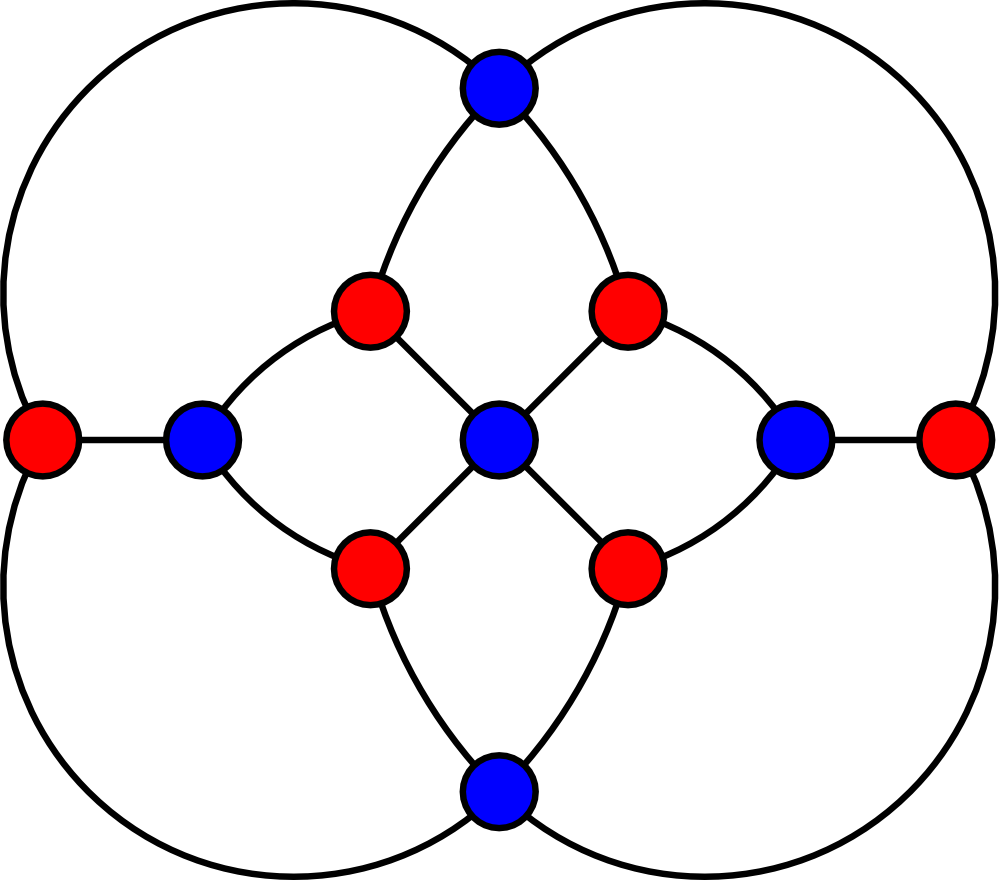
Graph theory is used in physics, chemistry, and computing.
Group theory is used in physics and chemistry, and computing.
Polyhedra turn up just about everywhere!
←
→
/
#
