ACE 8001: Quantitative Research
Methods:
An Outline
There are many reference sources to this topic. I choose only
two,
which are enough for the purposes of identifying the options and
appropriate
techniques to use in different circumstances and contexts:
- Alan Graham: Teach Yourself
Statisitics, Teach Yourself Books,
1993:
a basic text on descriptive statistics and presentation, including
helpful
advice on graphical analysis and presentation.
- Hair, Anderson, Tatham and Black: Multivariate Data Analysis,
Prentice
Hall International, 1998: a comprehensive textbook on the various
methods
of quantitative data analysis, how to use these methods and when they
are
appropriate.
A very useful online resource
is maintained by the University of
Surrey Sociology Department: Social Research Update.
This has links to a number of other important and useful sites, as well
as contiaing useful overview articles on various research approaches
and methods.
USEFUL LINKS:
Introduction
& Purpose
It is NOT the purpose of this session to fully aquaint or train you
in the use of these various methods - for that you will need to train
yourself
through the various computer packages and texts, and consult with
experts.
Rather, the purpose of this session is to provide an overview or
roadmap
of the various major techniques and approaches which are available.
These notes are in three sections:
Further sessions can be arranged (next term) with appropriate
members
of staff, given sufficient and specific demand to deal with particular
aspects of quantitative analysis. In particular, the methods
sessions
next term will deal with questionnaire design and implementation, and
also
deal with some case studies.
1. The Basics:
Positivism: The presumption (initial or founding assumption, or
axiom)
of a quantitative approach that the world (physical, biological, and
human
and social) is essentially systematic -
- it can be indentified and measured in objective
terms (unaffected
by individual sensations or emotions)
- relationships between the different parts of
these
worlds
can be established beyond reasonable doubt and independent of
subjective
judgement
- so that 'models' or theories of essential
behaviours and
indentities can be developed which explain and (possibly) predict
causal
effects - outcomes which depend on particular combinations of
pre-conditioning
circumstances.
This presumption - and its apparent diametric
opposition
to the qualitative approach dealt with in a companion session - is
further examined in the session on how and why we
think we can do research.
For the purposes of this session, we concentrate on the sorts of
concepts
and analyses which are common to the quantitative positivist approach,
though many of the basics and the methods apply to less rigid
applications than the strict postivist foundation.
Quantitative data
- data which can be sorted,
classified,
measured
in a strictly 'objective' way - they are capable of being accurately
described
by a set of rules or formulae or strict procedures which then make
their definition
(if not always their interpretation) unambiguous and independent of
individual
judgements.
- thus strictly replicable - they can be
re-collected
by someone else, somewhere else, and be expected to measure or identify
the same thing, and thus be directly comparable.
Such data are either CENSUS (containing measures for the Total or Whole
Population) or SAMPLE (relating only to the sub-set of then population
actually asked, surveyed, observed).
However, these statements are of ideals. In practice, many
apparently
quantitative data do depend critically on the way in which they were
collected,
who collected then, where they were collected, when they were collected
and from whom they were collected - they turn out not to be
replicable,
and turn out to be highly dependent on the circumstance and context of
their collection, and the character and culture of the collector. They
are, in short, biased.
In particular, sample data are likely to be biased simply because they
only relate to some (usually very small) sub-set of the total
population,
and thus may well accidentally reveal extreme rather than typical
values
for the population as whole. Much of formal statistics relates to
ways of testing whether or not sample data can be reliably used as
measures
of the whole population, while sampling methods seek to improve the
reliability
of sample data.
Nevertheless, they may still count as quantitative data IF the nature
of
the bias can be tested - if it can be established beyond
reasonable
doubt
(typically by statistical tests) that either the biases tend to
offset each other, so that collection and definition errors tend to
cancel
out, or that the bias is reliably (replicably) based on,
dependent
on, particular characteristics (quantitative measures) of the
differences
in the means and methods of collection.
In this case, the bias can be accounted
for.
In short - just because you have collected a number or a score or
characteristic,
or have found such a number, score, or character collected by someone
else,
does not mean that you have quantitative data. You may well have
collected qualitative data - which rely for their interpretation and
identification
on individual judgements about the ways in which they were collected,
and
the contexts and circumstances of their collection.
The ways in which data are collected are thus critical. Data
collection
is not to undertaken lightly.
Data Sources and Uses.
First, even if your major research focus is on qualitative data,
or even if it is a review of literature and organisation of concepts
(and
thus not focused on data as simple information at all) you will often
(if
not always) need to provide some background and context as
to why the issue you are addressing is important, and to whom it is
important.
This background will frequently require you to present some data to
illustrate
and describe the issue and its context. You will need to know something
about how to present data and what sorts of data you need. You will
frequently
need to re-phrase or re-present these data - so you will need (or need
to develop) some basic quantitative skills.
Good sources of background quantitative data - on the sizes
and
structures of the sectors, households, people, markets, economies,
societies
etc. - for the UK are:
- Annual Abstract of Statistics (HMSO) - the major population,
health,
economic
and market data series
- Social Trends (HMSO) - concentrating on social indicators
(health,
education,
ownership, crime etc.)
- Regional Trends (HMSO) - data available by regions of the country
Each of these three publications is actually a compilation of data
(statistics)
from a variety of different sources, all of which are referenced in
these
compendia, and many of which provide more detail if you need it. Those
interested in marketing and market intelligence should also be aware of
the Mintel database, available through the University Library system
(web
page). Please make sure that you follow the sensible rules about
using these data to illustrate the context and circumstances of your
study.
The key sensible rule is to think through what it is that the
data
say, which includes thinking through what it is they represent and how
they were collected. (See, e.g. Graham (ref. above) for advice
and
assistance on this.
Second: The sort of research you are doing determines your
need
to consider using quantitative approaches and techniques. Recall the
structure
of research approaches outlined earlier:
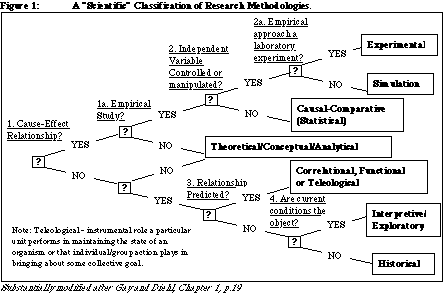
The only branch of this decision or organisational tree
which
does not readily admit of a quantitative approach is the
theoretical/conceptual/analytical
branch, though this branch (at least in physics and economics) does
depend
on formal logic systems and mathematics - presupposing that the world
to
which the theories relate is fundamentally measurable, and thus
susceptible
to quantitative approaches. All of the others can benefit from a
quantitative approach, while some (especially those on the upper
branches
and the correlational.. branch) demand a quantitative approach.
You
can only avoid quantitative approaches, in other words and according to
this taxonomy, by following the interpretive/exploratory or the
historical
route. Even then, some quantitative data and interpretation will
almost certainly make your analysis more robust.
The major constraint on adopting a quantitative approach, apart from
individual researcher preference or skill, is the availability of
appropriate
empirical data (information: facts and figures). If these do not exist
(as secondary data - already collected by someone else), then
you
will need to collect them as primary data.[Please note - data
are
plural, the singular is datum).
Third: - the road map:
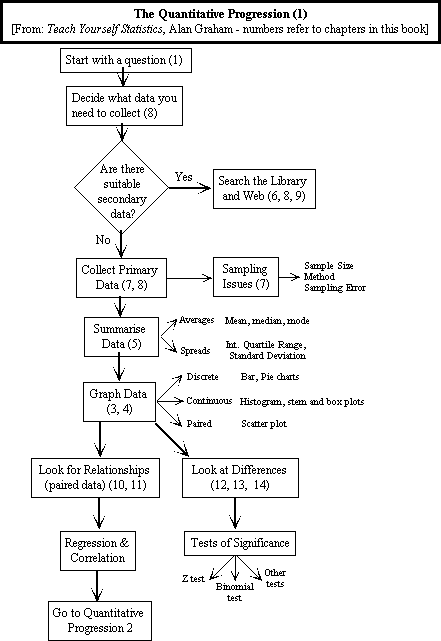
The economic approach to research is to rely on secondary data
if at all possible - it is cheaper and easier to get than primary data.
Some key points to remember when accumulating secondary data:
- Remember to source (note publication, table, page,
date,
author
or authority etc.) when collecting it - it is extremely frustrating
when
writing up if you forget where you got particular data from, and almost
impossible to find it again.
- Make sure you collect the data in the right (commensurate) units
- and note the units the numbers are in. If you are dealing with
economic
data (£s), make sure you know whether these are in real, volume
(constant
price), or nominal terms. Real means that the £s have
been
adjusted to eliminate the effects of general price inflation (usually
the
most useful and meaningful way of presenting time series data). Volume
or constant price data means that the effects of one (or a small
number)
of immediately relevant price changes have been excluded or eliminated
from the data - thus measuring the volume of the variable in question.
Nominal means the data are unadjusted for any price changes. For
international
comparisons, the units are important (the Americans often use short
tons
- 2000 lbs., not metric tonnes, and use bushels for measuring grains,
not
weight measures at all - so get the conversion tables).
- Make sure you understand the basics of where the data come from
and how
they are collected and defined. These sources and definitions
are
often contained in a separate publication. You need to know what the
data
mean, before you can use them sensibly, and you cannot know what they
mean
unless you know what they refer to.
Primary (typically Sample) Data:.
- Sample size - rule of thumb is that anything less than
30 is
practically
useless for any sort of quantitative statistical analysis. More is
better,
but the statistical benefits of increased sample size must be weighed
against
the costs of collection.
- Sample frame - the part of the whole relevant population
you
choose
to use to draw your sample - is it likely to be biased, and how might
you
be able to tell? Compare the averages (see below) of some common
features
(ages, genders, education levels, income bands etc.) with those of the
relevant population as a whole - frequently obtainable from the
secondary
data sources above. Use common sense in sampling - if you wish to
sample a shopping population, make sure that you cover the relevant
population
- only sampling during working hours will almost certainly give you a
biased
sample, as will only sampling during evenings or weekends. Think
about what you are doing.
- Sampling method - how are you choosing who to talk to or
question?
Randomly? Then you need a larger sample to cover the variation in the
population
of the things you are trying to measure. A Stratified Sample? - one
which
classifies the total population according to some well-defined criteria
(such as age, gender, place of work, etc.) and then seeks to make sure
that the sample contains a minimum number in each classification. This
is the way most opinion polsters work - with samples of 1000 or so to
represent
the total population of 52 million. Stratified samples allow us to draw
reliable (replicable) conclusions from smaller samples than entirely
random
samples.
- Sampling error - the smaller the sample (or the smaller
the
number
in each stratification), the larger will be the error.
Summarise Metric Data: (see below for a definition of metric)
- "Averages" - the central tendency or first moment of
the
distribution
of the sample. There are three different measures you should know about:
- Mean - arithmetic average as the sum of the
scores of each
observation divided by the number of observations. Sometimes (e.g.
average
price) a weighting system should be used - so that more sales at some
prices
rather than at others generate a greater weight for the more common
price
than the less common. In this case, the average price would be the
total
sales value divided by the total sales quantity (sometimes called the
unit
value) rather than the simple average of the price observed in each
period
(day, or week or whatever).
- Median - the mid point of the range
of
values observed (which divides the constellation of observations in
half, half the observations being on one side (less than) and half
being on the other side (more than)
- Mode - the most common value of the
variable
amongst the
whole distribution of values - the most frequently occuring value.
Depending on the shape of the distribution of values in the sample,
these
three measures will be different from each other. ONLY if the
distribution
is normal (i.e. bell-shaped) will the mean, mode and median all be the
same. This is not true for other distributional shapes. - Spreads:
the second moment of the distribution - a measure
of the
dispersion of the distribution. For a normal distribution, the variance
or standard deviation is an appropriate measure. For other
distributional
shapes, ranges and the spread of inter-quartile (or decile or other
fractional)
ranges is more informative of the shape of the distribution.
- Graphs: Depend on the nature of the data -
- use bar, pie or column charts for discrete data (ones which
have
specific
values - e.g. 1, 2, 3 .., or which are ordinal (rankings) or are
non-metric
- signifying possession or absence of a particular attribute);
- use histograms, or line charts, or stem and box plots for
continuous
data,
where the variable in question could exhibit any value;
- use scatter plots (one category or variable against the other)
for
paired
variables.
Beware the optical illusions possible through changing the
scales
and dimensions of graphs - making some trends or variations seem either
more pronounced or less important than otherwise. Any pictorial
representation
of data is often more immediately comprehensible by the reader - but
you
need to take care to leave the reader with the reliable and defensible
impression of the nature of the data, and not with an illusion. - Significance
Tests: Because any sample will automatically
throw
up either apparent differences between and/or apparent associations
between
variables simply by chance, it is often important to test whether or
not
these apparent differences or similarities are just due to chance or
whether
we can bet that they betray some genuine underlying pattern. The
statisticians
have developed a number of statistical tests to provide the information
on reliability of apparent differences and associations - look up
the
one you need for particular circumstances. These tests are
especially
important if you intend to base any subsequent analysis or conclusions
on the apparent differences or similarities you think you may have
found.
Summarise non metric or categorical data:
- Graph proportions: what proportion of the total
sample (population)
is characterised in particular quantitative ways.
- Compare proportions between different samples
- Compare proportions of one or more particular characteristics
with
others.
Useful resources for social surveys:
- The Question Bank
(a
site provided
by the Department of Sociology, University of Surry, who, in
conjunction
with the University of Southampton also run the ESRC Centre for
Applied
Social Surveys (CASS)
2. Data Analysis:
You need to think through what you are going to do with data BEFORE
you rush out to collect it.
Data is simply information - it is neither knowledge nor
understanding
until you analyse it - sort it out into meanings: relationships,
correlations, associations.
The sort of relationships you are looking for determine the sorts of
statistical methods you can use to test the relationships, and also
determine
the sort of data you need to find or collect.
Simply collecting data without any plan of what you are looking for and
how you are going to use what you collect is not science, it is not
research,
it is simply collecting - don't expect to be given either many marks or
much respect for simply collecting information. Squirrels do that
- and even they collect nuts for a purpose.
If you collect data before you know how you are going to use it, 'sods
law' will operate - and you will discover you have either wasted a lot
of time collecting data you cannot use, or have failed to collect the
really
vital bit of information, or, most likely, both at the same time.
Caveat: this section of notes may be offputting
to many of you. It is deliberately dense and brief. It is
designed
as a reference source, and you are not intended to learn this - you
simply
need to know that it exists, and that you can use it as and when your
particular
research (either now or in the future) needs to use it.
The key to satisfactory and successful analysis is the conceptual
design of the research. I find the metaphor of tidying up a bedroom
or office helpful. The room looks like a bomb-site, with things and
objects
(and even people) all over the place in complete chaos. It is
information
without any knowledge or understanding. Sorting it out and tidying it
up
requires some organising plan - a set of boxes or places to put things
which are related or similar and keep them separate from those which
are
less related or less similar. Typically we start the process without a
clear plan, and develop a series of classifications as we go along -
discovering
that our first attempts were misconceived. In addition, we keep getting
side-tracked - picking up things we never knew we had and sitting down
to mend, read or use them instead of continuing with the tidying.
The objective of the tidying up is to make the room easier and
better
to live in - so that it works better - we can find what we need and the
the things we need to be together are together. But the appropriate
places
and organisation depend on how we live and what we like. What suits us
may not suit other people. Nevertheless, there are common models or
best-practices
which have emerged through time which suggest that some forms of
orgaisation
are more generally acceptable and useful than others.
In research, we typically begin with some understanding of the
existing
common models or best-practices - from the literature. We then refine
and
re-define these to better suit our own particular purposes - what sort
of room is it we wish to develop? How are we going to use the results?
So, what sort of results do we need and how robust and reliable do the
results need to be?
We need to decide what it is we are trying to do. We
need
to decide what particular aspects of the things we are looking at are
important,
and what can be ignored. What do we need to know about the world? What
can we measure or recognise? Things (actions and people) come as
bundles
of attributes and attitudes. Observations of these things will be variable
-
the scale, pattern, or mixture of attributes and attitudes will vary
depending
on which thing we are looking at (and where and when we look at it).
The
particular attributes or attitudes we choose to concentrate on will
vary
between things (actions and people). We call these characteristics
variables
- any given observation will consist of one or more of particular
values
of these variables - either metric values (size or rank
(order))
or nonmetric values (a category, such as gender, social class,
occupation
etc.). The values of the variables become our data.
There are three key, critical questions we need to ask
about
our data - the mess in the room.
- can the variables (the boxes into which we put the things, which
are
our
observations) be divided into dependent and independent types based on
some theory or story about the way the world (room) works? Are some
groups
of things - the variables - pre-determined by other groups of things or
not? If they are, then we are dealing with a dependent system.
If
not, then we are dealing with an interdependent system, where
everything
depends on everything else. [To suppose that nothing is related to
anything
else denies the possibility of any sort of analysis or tidying up.]
- If we are dealing with a dependent system, how many of
the
variables
are to be treated as dependent - they cannot all be dependent,
otherwise
we have an interdependent system.
- Finally, how are we defining our variables (boxes) - can we
measure the
thing to decide whether or not it belongs in a box? If so, then it is a
metric variable
- it has a size or a rank. If not, then we can only type it,
classify
it as being something or not, as having a particular attribute or not,
it is nonmetric - it is either one thing or another - defined
as
a category, a categorical definition - like gender (unless we think of
gender as a continuous phenomenon over a complete spectrum from
outright
macho maleness to ...?, rather than a categorical condition).
These three questions ultimately determine the most appropriate method
for tidying up the roomfull of observations. Having chosen which
particular
data we are going to collect (observe and measure or classify), or
having
already got some particular data set (collection of observations), the
answers to these questions then determine what sort of analysis is most
appropriate.
Hair et al. provide a map for the determination of which
analytical
approach we need:
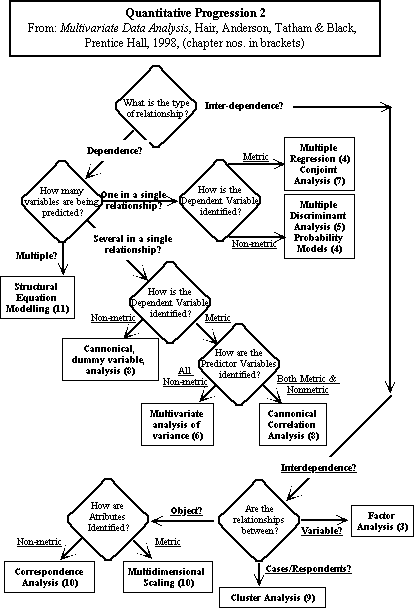
Hair et al. (p 19) outline the relationships between the various
multivariate
approaches for the dependence branches in the above tree as follows:
| Method |
Dependent Variables (=) |
Independent or explanatory variables |
| Connonical Correlation |
Y1, Y2, Y3, ..(metric and non-metric) |
X1, X2, X3, .. (metric and nonmetric) |
| Mutivariate Anova (Anal. of Var.) |
Y1, Y2, Y3, ..(metric) |
X1, X2, X3, .. (nonmetric) |
| Anal. of Var. |
Y1 (metric) |
X1, X2, X3, .. (nonmetric) |
| Mutiple Discriminant Analysis |
Y1 (nonmetric) |
X1, X2, X3, .. (metric) |
| Mutiple Regression Analysis |
Y1 (metric) |
X1, X2, X3, .. (metric and nonmetric) |
| Conjoint Analysis |
Y1 (metric and nonmetric) |
X1, X2, X3, .. (nonmetric) |
| Structural Equation Modelling |
Y1 (metric) =
Y2 (metric) =
Y3 (metric) =
|
X11, X12, X13 .. (metric and nonmetric)
X21, X22, X23 .. (metric and nonmetric)
X31, X32, X33 .. (metric and nonmetric)
|
For interdependence conceptions of the way the world is, the
key distinction is the focus of the analysis on the type of
inter-relationship.
If the focus is on classifying groups of people (or things) as groups
of
objects defined according to multivariate dimensions, then
multidimensional
scaling or correspondence analysis should be used, depending on whether
or not the dimensions are considered to be metric or nonmetric. These
techniques
group objects according to the distances displayed by each object on
each
dimension, where the dimensions themselves are pre-specified by the
researcher.
Cluster analysis is a technique which seeks to identify the relevant
dimensions by grouping cases/respondents according to their overall
similarity
or differences according to the measured dimensions of the variables
observed.
Factor analysis seeks to condense a large number of variables into a
smaller number of factors (sometimes called variates - as groups of
variables)
which underly the relationships shown between the variables across the
respondents or cases.
3. CONCLUDING
REMARKS
-
IS THERE REALLY A RELIABLE DISTINCTION BETWEEN
QUALITATIVE
AND QUANTITATIVE DATA AND RESEARCH?
Those who have been thinking about these notes, and comparing them with
the companion session on 'Qualitative' research, will have
noticed
that the distinction between quantitative and qualitative techniques is
pretty messy and indistinct. It is perfectly possible to develop
more or less plausible and definsible arguments that any and all data
are
either inherently qualitative or inherently quantitative.
To be sure, quantitative researchers typically rely heavily on
statistical
techniques, and spend a lot of time with computational algorithms and
software
packages trying to get their data to tell the truth. Qualitative
researchers, on the other hand, spend their time poring over
transcripts
or recordings of interviews, detailed notes of focus groups or
participant
research, etc., similarly trying to get their data to tell the
truth.
But are their methods really so different? They are both looking
for bias, reliability, replicability, objectivity, scientific rigour
etc.
Perhaps a better and more useful distinction is between those who
rely
on EXTENSIVE research - collecting information on a few apparently
salient
characteristics and measures of lots of people, or events; and those
who
rely on INTENSIVE research - collecting a large amount of detailed
information
on diverse characteristics about rather few people and events.
Even
then, it is not the data, as such, which distinguish these different
research
approaches - rather it is typically their view of the way the world
works,
or the ways in which the workings of the world can be best observed,
examined
and understood.
Such considerations should lead us to think more carefully
about
what it is that social science is actually trying to do, and whether or
not it has any chance of doing it. My
companion session trys to deal with these questions. Here,
the
thinking
becomes
especially philosophical, which is not to everyone's taste.
However,
you should all at least be aware (beware) of these rather fundamental
questions,
since they underpin everything we think of as research - and thus
everything
we think of. Yes, this is tough stuff - but this is a Master's
course,
and people with an MSc or MA should be able to tackle tough questions
and
make some sense of them. Otherwise, what is the point?
Otherwise,
why should you expect other people to take you seriously and respect
your
qualification?
Back to top
Back to DRH Page
Comments and suggestions
to DRH