8 Logistic Regression
The logistic regression test in CASSI is essentially the same as the epistasis test as implemented in PLINK Purcell et al. (2007). The difference being that CASSI uses the likelihood ratio test between logistic regression models with and without an interaction term. Furthermore, CASSI has the added bonuses of running much faster (see section 10.3) and being able to incorporate covariates into the analysis, as well as being able to use any other test in CASSI as a screening step.
The options that are specific to the logistic regression test are:
| Option | Description |
|---|
| -lr | perform the logistic regression test |
| -lr-th t | p-value threshold for the logistic regression test |
| -lr-so | suppress results of test |
| -lr-covar covariates.dat | set covariate file, covariates.dat |
| -lr-covar-number nums | only use covariates given by the numbers, nums |
| -lr-covar-name na | only use covariates given by the names, na |
| -lr-covar-miss x | set missing covariate value, x |
The default p-value threshold is 0.0001 and the default missing covariate value is -9.
For other basic options see section 3.2.
The output file from running a logistic regression epistatis analysis using CASSI will look something like the following:
SNP1 CHR1 ID1 BP1 SNP2 CHR2 ID2 BP2 LR_LOG_OR LR_SE LR_CHISQ LR_P
541 1 rs2657274 4518966 783 1 rs7931851 5254756 0.37203 0.0946377 15.4536 8.45579e-05
542 1 rs2657273 4519034 783 1 rs7931851 5254756 0.422308 0.0973076 18.8349 1.42531e-05
544 1 rs2641314 4519523 783 1 rs7931851 5254756 0.423179 0.0963309 19.2982 1.11809e-05
556 1 rs1505116 4535285 637 1 rs1732891 4800616 -1.41948 0.364753 15.1446 9.95837e-05
609 1 rs7117459 4708712 621 1 rs1278492 4750695 17.9602 4.54453 15.6186 7.74883e-05
...
The first line is a header labelling the columns of the results file. The SNP details for the pair of SNPs are given firstly followed by values calculated from the logistic regression test.
LR_LOG_OR is the log odds ratio for interaction.
LR_SE is the standard error of LR_LOG_OR (given by assuming LR_LOG_OR squared divided by its variance approximates the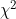 
test statistic).
LR_CHISQ is the 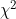test statistic with one degree of freedom.
LR_P is the corresponding p-value.
It is possible to perform the logistic regression test with a set of covariates. To do this use the -lr-covar option. For example:
./cassi -lr -lr-covar covariates.dat mydata.bed
Unfortunately, the logistic regression test with covariates is very s-s-s-s-slow (see section 10.3), so a large analysis is not advisable. However, this is not a problem as any other test in CASSI can be used as a screening step before performing logistic regression with covariates. See section 10 for details.
The format of the covariate file is the same as PLINK covariate files. That is, a text file where the first column is the pedigree ID, the second column is the individual ID and the remaining columns are the covariate values, where a value of -9 denotes a missing value (this may be changed with the -lr-covar-miss option). For example, a covariate file with 3 covariates may look as follows:
PEDID ID SMOKE ALCOHOL EX
WXA_T123 QWA_T120 0.0032 0.0033 0.0207
WXA_T123 QWA_T121 -0.0019 0.022 0.0247
WXA_T124 QWA_T987 0.0104 0.0096 -0.0154
...
The header line may be present or not. The covariates may be chosen with the header names as follows:
./cassi -lr -lr-covar covariates.dat -lr-covar-name ALCOHOL,EX -o myresults.dat mydata.bed
or
./cassi -lr -lr-covar covariates.dat -lr-covar-name ALCOHOL-EX -o myresults.dat mydata.bed
to include all covariates between and including these two. Note that no spaces should be used between the chosen covariate values. The covariates may also be chosen by their numbers. So the above may be written:
./cassi -lr -lr-covar covariates.dat -lr-covar-name 2,3 -o myresults.dat mydata.bed
or
./cassi -lr -lr-covar covariates.dat -lr-covar-name 2-3 -o myresults.dat mydata.bed
The output file from running a logistic regression analysis with covariates will look something like the following:
SNP1 CHR1 ID1 BP1 SNP2 CHR2 ID2 BP2 LR_COVAR_LOG_OR LR_COVAR_SE LR_COVAR_CHISQ LR_COVAR_P
135 1 rs1627458 1633498 297 1 rs451041 3017301 0.381645 0.091521 17.3892 3.04559e-05
135 1 rs1627458 1633498 299 1 rs711857 3024682 0.388182 0.0932027 17.3466 3.11453e-05
143 1 rs1627507 1673325 216 1 rs794012 2549107 2.60804 0.665518 15.3571 8.89863e-05
166 1 rs2107425 1977651 203 1 rs108134 2459062 0.574884 0.146822 15.3313 9.02099e-05
200 1 rs7570914 2397565 371 1 rs267216 3648600 0.726192 0.184818 15.4388 8.52196e-05
...
That is, it is the same as before but with a different header, which is useful when performing logistic regression with and without covariates.
