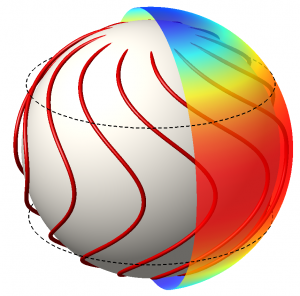
From helioseismology it is known that the Sun’s radiation zone rotates as a solid body, whereas the convection zone rotates differentially — slower at the poles and faster at the equator. The shear layer in between is known as the ‘tachocline’.
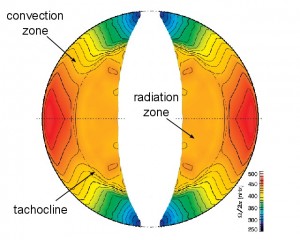
(Korzennik & Eff-Darwich 2011).
The solid rotation of the radiation zone can be explained by the presence of a global-scale magnetic field, in accordance with Ferraro’s law of isorotation. This field must be confined to the radiation zone, i.e., prevented from diffusing out into the convection zone.
The differential rotation of the convection zone is maintained by the transport of angular momentum by convective turbulence. The convection zone exerts a retrograde drag on the high-latitude tachocline, which drives meridional flows that try to burrow into and thereby spin down the interior. To prevent this burrowing, the magnetic field must transport angular momentum to the poles from lower latitudes.
My research concerns the processes that confine the interior magnetic field below the convection zone, and the transport of angular momentum by the magnetic field in the tachocline.
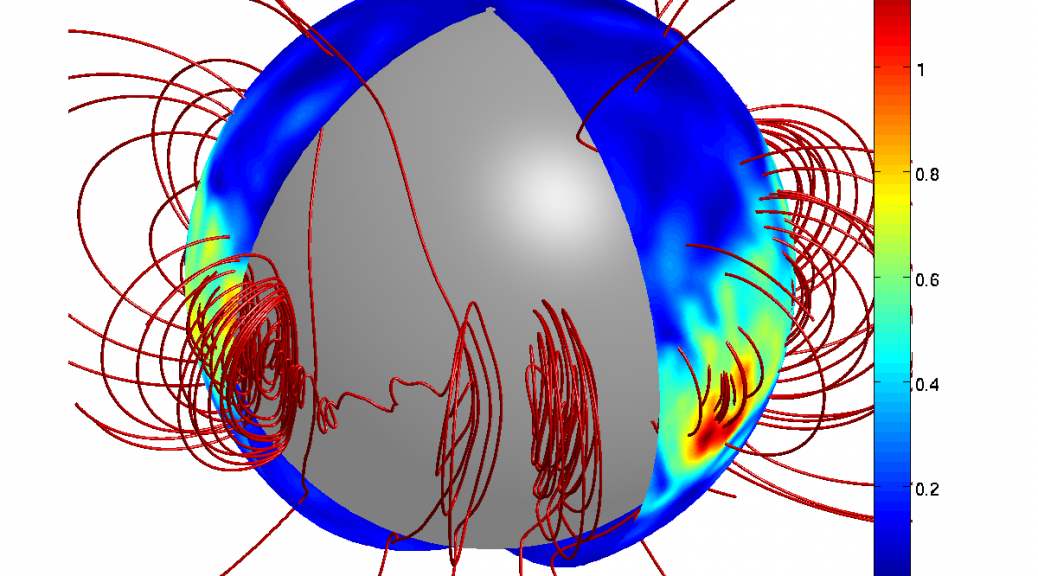
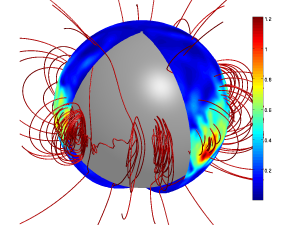
In middle and low latitudes the internal magnetic field can be confined by “magnetic pumping” by overshooting convective plumes. In high latitudes the field must be confined by the tachocline’s meridional flow, which is expected to be downwelling near the pole.

(Wood & Brummell 2018, ApJ, 853, 97)
In middle latitudes, the shear within the tachocline winds up the magnetic field lines, transmitting a prograde Maxwell torque to the poles that maintains the solid rotation of the radiation zone.